Câu hỏi:
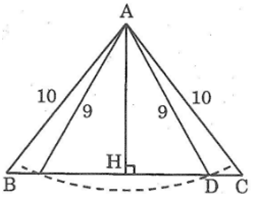
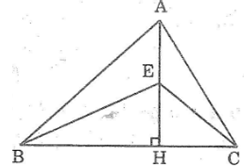
19/04/2020 5,287Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không, có cắt cạnh BC hay không? Vì sao?
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Kẻ AH ⊥ AB.
Xét hai tam giác vuông AHB và AHC, ta có:
∠AHB = ∠AHC = 90o
AB = AC (gt)
AH cạnh chung
Suy ra: ΔAHB = ΔAHC
(cạnh huyền - cạnh góc vuông)
Suy ra: HB = HC (hai cạnh tương ứng)
Ta có: HB = HC = BC/2 = 6 (cm)
Trong tam giác vuông AHB có ∠AHB = 90o
Áp dụng định lí Pi-ta-go, ta có:
AB2 = AH2 + HB2 ⇒ AH2 = AB2 – HB2 = 102 – 62 = 64
⇒ AH = 8 (cm)
Do bán kính cung tròn 9(cm) > 8(cm) nên cung tròn tâm A bán kính 9 cm cắt đường thẳng BC.
Gọi D là giao điểm của cung tròn tâm A bán kính 9 cm với BC.
Vì đường xiên AD < AC nên hình chiếu HD < HC.
Do đó D nằm giữa H và C.
Vậy cung tròn tâm A bán kính 9 cm cắt cạnh BC.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
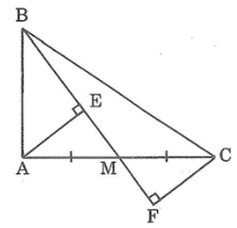
Trong ΔABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM (trong tam giác vuông cạnh huyền lớn nhất)
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ΔAEM = ΔCFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2 .
Lời giải
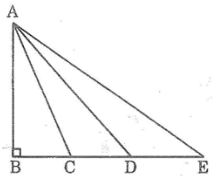
+ Ta có BC < BD < BE.
Mà AC, AD, AE là các đường xiên tương ứng với các hình chiếu BC, BD, BE
Suy ra AC < AD < AE.
+ AB là đường vuông góc nên AB nhỏ nhất trong tất cả các đường xiên và đường vuông góc.
Do đó AB < AC < AD < AE.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2