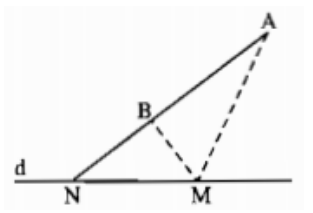
Cho đường thẳng d và hai điểm A, B nằm cùng một phía của d và AB không song song với d. Một điểm M di động trên d. Tìm vị trí của M sao cho |MA−MB| là lớn nhất
Câu hỏi trong đề: Sách bài tập Toán 7 Tập 2 !!
Quảng cáo
Trả lời:
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Theo hệ quả bất đẳng thức tam giác ta có:
|MA−MB| < AB
Khi M ≡ N thì
|MA−MB|= AB
Vậy |MA−MB| lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
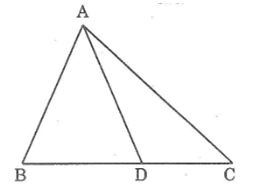
Trong ΔABD, ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ΔADC, ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2), ta có:
2AD < AB + BD + AC + DC ⇔ 2AD < AB + AC + BC
Vậy AD < (AB + AC + BC) / 2 .
Lời giải
Giả sử ΔABC có AB = 7cm, AC = 2cm.
Theo định lý và hệ quả của bất đẳng thức tam giác, ta có:
AB - AC < BC < AB + AC
⇒ 7 - 2 < BC < 7 + 2 ⇔ 5 < BC < 9
Vì số đo cạnh BC là một số tự nhiên lẻ nên BC = 7 (cm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.