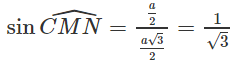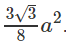Tính sin của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều.

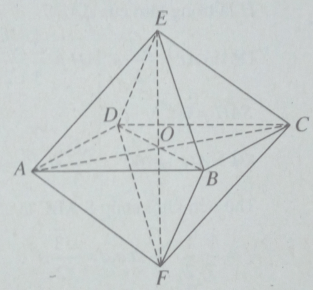
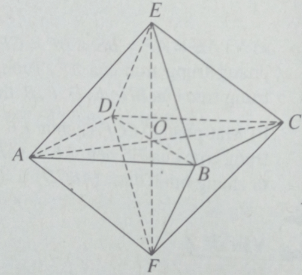
Ta có khối bát diện đều ABCDEF như hình vẽ. Gọi O là giao điểm của EF và (ABCD). Khi đó mặt phẳng (ABCD), điểm O và đường thẳng EF lần lượt là mặt phẳng đối xứng, tâm đối xứng và trục đối xứng của khối bát diện đều đã cho.

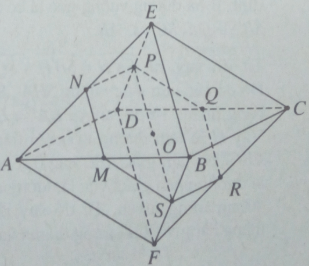
Ta có khối bát diện đều ABCDEF, cạnh a. Do MN // (DEBF) nên giao của mặt phẳng (OMN) với mặt phẳng (DEBF) là đường thẳng qua O và song song với MN.

Ta nhận thấy đường thẳng này cắt DE và BF tại các trung điểm P và S tương ứng của chúng. Do mặt phẳng (ADE) song song với mặt phẳng (BCF) nên (OMN) cắt (BCF) theo giao tuyến qua S và song song với NP. Dễ thấy giao tuyến này cắt FC tại trung điểm R của nó. Tương tự, (OMN) cắt DC tại trung điểm Q của nó. Từ đó suy ra thiết diện tạo bởi hình bát diện đã cho với mặt phẳng (OMN) là lục giác đều có cạnh bằng a/2.

Do đó diện tích của nó bằng