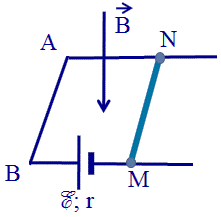
Trong một mặt phẳng nghiêng góc a so với mặt phẳng nằm ngang, có 2 thanh kim loại cố định song song cách nhau một khoảng l, nối với nhau bằng một điện trở R; tất cả được đặt trong một từ trường đều không đổi B vuông góc với mặt phẳng chứa hai thanh và hướng lên phía trên (như hình vẽ).
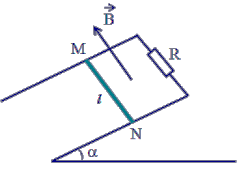
Một thanh kim loại MN, có khối lượng m, có thể trượt không ma sát trên hai thanh kia và luôn luôn vuông góc với chúng. Điện trở của các thanh không đáng kể. Người ta thả cho thanh MN trượt không có vận tốc ban đầu.
a) Mô tả hiện tượng và giải thích tại sao vận tốc v của MN chỉ tăng tới giá trị cực đại . Tính (giả thiết hai thanh song song có chiều dài đủ lớn).
b) Thay điện trở bằng một tụ điện có điện dung C. Chứng minh rằng lực cản chuyển động tỉ lệ với gia tốc a của thanh. Tính gia tốc này. Cho gia tốc trọng trường bằng g.
Quảng cáo
Trả lời:
a) Mô tả hiện tượng và giải thích
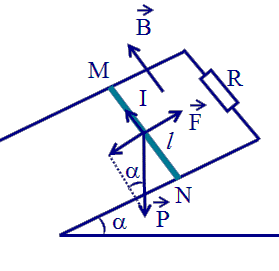
Khi thanh MN trượt xuống dưới tác dụng của trọng lực, từ thông qua diện tích MRN biến thiên, trong mạch xuất hiện suất điện động cảm ứng ; với v là vận tốc trượt của thanh; dòng điện cảm ứng có chiều từ N đến M và có cường độ:
Thanh chịu tác dụng của các lực:
Lực từ và trọng lực P = m.g.
Khi lực từ còn nhỏ hơn thành phân của trong lực trên mặt phẳng nghiêng P.sina thì thanh chuyển động nhanh dần, vân tốc v tăng và lực từ F tăng.
Khi lực từ cân bằng với thành phần của trọng lực trên mặt phẳng nghiêng thì vật chuyển động đều và vận tốc thanh đạt được lúc đó là cực đại.
Tính vận tốc cực đại đó
Ta có:
b) Thay điện trở bằng một tụ điện có điện dung C
Dòng cảm ứng nạp điện vào tụ.
Điện tích tức thời của tụ:
Lực cản
Vậy F tỉ lệ với a.
Tính a:
Phương trình chuyển động của thanh:
Gia tốc a nhỏ hơn gia tốc trượt khi không có từ trường B, và phụ thuộc vào khối lượng m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
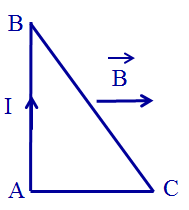
Lực từ tác dụng lên cạnh AC là = vì AB song song với .
Lực từ tác dụng lên cạnh AB là có điểm đặt tại trung điểm của AB, có phương vuông góc với mặt phẳng chứa khung dây, hướng từ ngoài vào như hình vẽ.
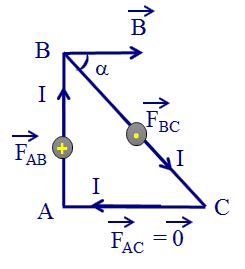
Có độ lớn:
Lực từ tác dụng lên cạnh BC là có điểm đặt tại trung điểm của BC, có phương vuông góc với mặt phẳng chứa khung dây, hướng từ trong ra và có độ lớn:
Lời giải
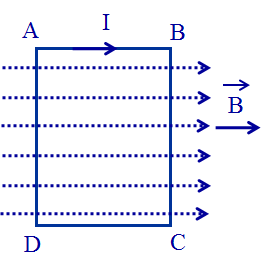
Các cạnh AB và CD song song với các đường sức từ nên lực từ tác dụng lên các cạnh này bằng 0. Lực từ tác dụng lên các cạnh BC và AD có điểm đặt tại trung điểm của mỗi cạnh, có phương vuông góc với mặt phẳng khung dây, lực tác dụng lên cạnh BC hướng từ trong ra ngoài, lực tác dụng lên cạnh AD hướng từ ngoài vào trong như hình vẽ.
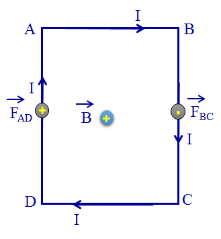
Có độ lớn:
Hai lực này tạo thành một ngẫu lực có tác dụng làm cho khung dây quay đến vị trí mà mặt phẳng khung dây vuông góc với các đường sức từ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.