Câu hỏi:

11/07/2024 4,592

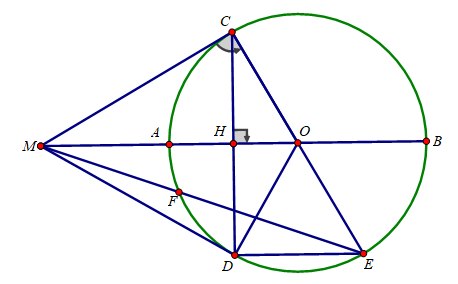
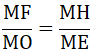Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
d) ME cắt đường tròn (O) tại F (khác E). Chứng minh: ∠(MOF) = ∠(MEH )

Xem lời giải

Câu hỏi trong đề: Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đề kiểm tra Toán 9 | Đề thi Toán 9

d) Ta có: ∠(CFE) = $90^{0}$ (F thuộc đường tròn đường kính CE)

Lại có CF là đường cao nên ${MC}^{2}$ = MF.ME

Tương tự, ta có: ${MC}^{2}$ = MH.MO

⇒ ME.MF = MH.MO

⇒ Đề kiểm tra Toán 9 | Đề thi Toán 9

Xét ΔMOF và ΔMEN có:

Đề kiểm tra Toán 9 | Đề thi Toán 9

∠(FMO) chung

⇒ ΔMOF ∼ ΔMEN (c.g.c)

⇒ ∠(MOF) = ∠(MEH)

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Cấp tốc 789+ thi vào lớp 10 môn Toán

Đã bán 261

₫ 195.000 ₫ 95.000

Hà Nội

Cấp tốc 789+ thi vào lớp 10 môn Ngữ Văn

Đã bán 111

₫ 180.000 ₫ 97.000

Hà Nội

Cấp tốc 789+ thi vào lớp 10 môn Tiếng Anh

Đã bán 1k

₫ 180.000 ₫ 97.000

Hà Nội

Lớp 9 - Siêu trọng tâm Toán, Văn, Anh

Đã bán 411

₫ 180.000 ₫ 97.000

Hà Nội

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Giải phương trình
b) $\sqrt{4 x - 12} + \frac{1}{3} \sqrt{9 x - 27} - 2 \sqrt{\frac{x - 3}{4}} = 4$

Xem đáp án » 11/07/2024 8,869

Câu 2:

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
a) Chứng minh MD là tiếp tuyến của đường tròn (O).

Xem đáp án » 11/07/2024 8,483

Câu 3:

Cho hàm số y = –2x + 3 có đồ thị (d1) và hàm số y = x – 1 có đồ thị ( $d_{2}$ )
b) Xác định hệ số a và b biết đường thẳng ( $d_{3}$ ): y = ax + b song song với ( $d_{2}$ ) và cắt ( $d_{1}$ ) tại điểm nằm trên trục tung.

Xem đáp án » 11/07/2024 8,109

Câu 4:

Cho biểu thức :
$A = \frac{15 \sqrt{x} - 11}{x + 2 \sqrt{x} - 3} + \frac{3 \sqrt{x} - 2}{1 - \sqrt{x}} - \frac{3}{\sqrt{x} + 3}$ $(x \geq 0; x \neq 1)$
a) Thu gọn biểu thức A.

Xem đáp án » 11/07/2024 5,881

Câu 5:

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
b) Kẻ đường kính CE của đường tròn (O). Tính MC, DE theo R.

Xem đáp án » 11/07/2024 4,504

Câu 6:

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
c) Chứng minh $H A^{2} + H B^{2} + C D^{2} / 2 = 4 R^{2}$

Xem đáp án » 11/07/2024 4,021

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Giải phương trìnhb) 4x-12+139x-27-2x-34=4

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.a) Chứng minh MD là tiếp tuyến của đường tròn (O).

Cho hàm số y = –2x + 3 có đồ thị (d1) và hàm số y = x – 1 có đồ thị (d2)b) Xác định hệ số a và b biết đường thẳng (d3): y = ax + b song song với (d2) và cắt (d1) tại điểm nằm trên trục tung.

Cho biểu thức :A=15x-11x+2x-3+3x-21-x-3x+3x≥0;x≠1a) Thu gọn biểu thức A.

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.b) Kẻ đường kính CE của đường tròn (O). Tính MC, DE theo R.

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.c) Chứng minh HA2+HB2+CD2/2=4R2

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Giải phương trình
b) $\sqrt{4 x - 12} + \frac{1}{3} \sqrt{9 x - 27} - 2 \sqrt{\frac{x - 3}{4}} = 4$

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
a) Chứng minh MD là tiếp tuyến của đường tròn (O).

Cho hàm số y = –2x + 3 có đồ thị (d1) và hàm số y = x – 1 có đồ thị ( $d_{2}$ )
b) Xác định hệ số a và b biết đường thẳng ( $d_{3}$ ): y = ax + b song song với ( $d_{2}$ ) và cắt ( $d_{1}$ ) tại điểm nằm trên trục tung.

Cho biểu thức :
$A = \frac{15 \sqrt{x} - 11}{x + 2 \sqrt{x} - 3} + \frac{3 \sqrt{x} - 2}{1 - \sqrt{x}} - \frac{3}{\sqrt{x} + 3}$ $(x \geq 0; x \neq 1)$
a) Thu gọn biểu thức A.

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
b) Kẻ đường kính CE của đường tròn (O). Tính MC, DE theo R.

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.
c) Chứng minh $H A^{2} + H B^{2} + C D^{2} / 2 = 4 R^{2}$