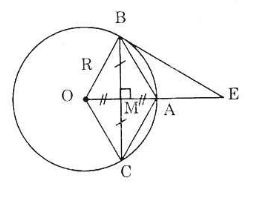
Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.
a) Tứ giác OCAB là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
b) Ta có: OA = OB (bán kính)
OB = BA (tính chất hình thoi).
Nên OA = OB = BA => ΔAOB đều
Trong tam giác OBE vuông tại B ta có:
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
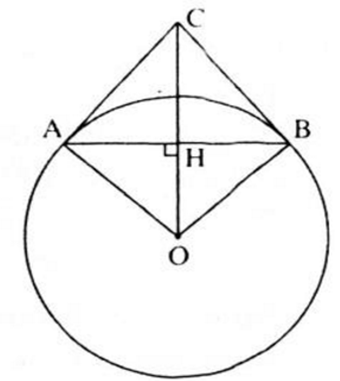
a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)
Vậy OC = 25 cm
Nhắn tin Zalo