Câu hỏi:
05/04/2025 6,785Cho hình thang ABCD có đáy lớn CD là 20 cm, đáy nhỏ AB là 15 cm. M là một điểm trên AB cách B là 5 cm. Nối M với C. Tính diện tích hình thang mới AMCD. Biết diện tích tam giác MBC là 280 cm2.
Câu hỏi trong đề: Hình học !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
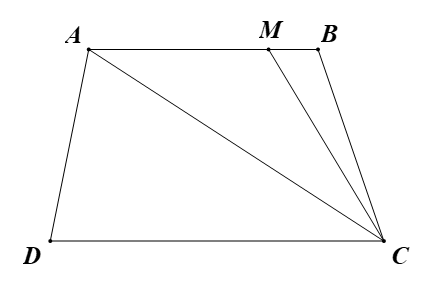
Cách 1:
Đáy mới AM là: 15 – 5 = 10 (cm)
Tổng hai đáy AM và CD là: 10 + 20 = 30 (cm)
Chiều cao hình thang AMCD là: 280 × 2 : 5 = 112 (cm)
Diện tích hình thang AMCD là: 30 × 112 : 2 = 1680 ()
Đáp số: 1680
Cách 2:
Nối A với C.
Ta có đoạn AM là: 15 – 5 = 10 (cm)
Diện tích tam giác ACM gấp 2 lần điện tích tam giác MCB ⇒ Diện tích tam giác ACM = 280 × 2 = 560 () (vì AM gấp hai lần BM và đường cao hai tam giác bằng nhau)
∆DAC và ∆MCB, có:
⦁ DC gấp MB là:
20 : 5 = 4 (lần)
⦁ Đường cao chung nên diện tích tam giác DAC gấp 4 lần diện tích tam giác MCB.
Diện tích tam giác ADC là: 280 × 4 = 1120 ()
Diện tích hình thang AMCD là:
1120 + 560 = 1680 ()
Đáp số: 1680 .
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có 3 cặp tam giác có diện tích bằng nhau là
S ADB = SABC (vì cùng đáy AB x chiều cao chia 2)
SACD = SBCD
SAID = SIBC
Vì chúng đều là phần diện tích còn lại của 2 tam giác có diện tích bằng nhau và có chung 1 phần diện tích. (Tam giác ICD hoặc AIB)
Lời giải
MQ kéo dài cắt DC tại F; MN kéo dài cắt DC tại E
Ta có diện tích hình thang ABCD bằng diện tích tam giác FME
S∆ MPF = S∆ MPE (đáy bằng nhau, đường cao chung)
S∆ MNP = S∆NPE (đáy MN = NE, đường cao chung)
S∆PMQ = S∆PQF (đáy MN = NE, đường cao chung)
Nên SMNPQ = 1/2 S ∆FME hay S(MNPQ) =1/2 S(ABCD)
= 60 : 2 = 30 (cm2)
Đáp số: 30 cm2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán lớp 5 Kết nối tri thức có đáp án - Đề 1
-
15 câu trắc nghiệm Toán lớp 5 Kết nối tri thức Ôn tập số tự nhiên có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán lớp 5 Kết nối tri thức có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán lớp 5 Chân trời sáng tạo có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán lớp 5 Kết nối tri thức có đáp án - Đề 3
-
Bộ 5 đề thi cuối kì 2 Toán lớp 5 Cánh diều có đáp án - Đề 1
-
Bộ 15 đề thi ôn vào lớp 6 môn Toán chất lượng cao năm 2024 - 2025 có đáp án (Đề 1)
-
Bộ 10 đề thi cuối kì 2 Toán lớp 5 Kết nối tri thức có đáp án - Đề 2
Nhắn tin Zalo
Trí Hoàng
Nó hơi lố, chiều cao 112 cm???????????