Cho định lý: “Hai góc cùng phụ với một góc thứ ba thì bằng nhau”. Hãy điền từ thích hợp vào chỗ trống để hoàn tất chứng minh định lý
- Ta có: (do hai góc kề bù)
- Ta lại có: ( do hai góc kề bù)
(2)
Từ (1) và (2) suy ra: .
A.
B.
C.
D.
Quảng cáo
Trả lời:
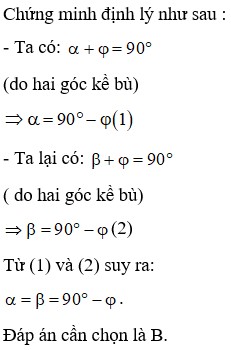
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 3 – 2 – 4 – 5 – 6 – 1
B. 3 – 4 – 2 – 5 – 6 – 1
C. 3 – 2 – 5 – 4 – 6 – 1
D. 3 – 4 – 5 – 2 – 6 – 1
Lời giải
Thứ tự đúng là: 3 – 2 – 5 – 4 – 6 – 1
Đáp án cần chọn là C.