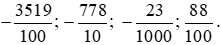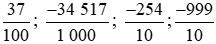Thực hành 3 trang 31 Toán lớp 6 Tập 2:
a) Hãy sắp xếp các số thập phân sau theo thứ tự tăng dần:
−12,13; −2,4; 0,5; −2,3; 2,4.
b) Hãy sắp xếp các số thập phân sau theo thứ tự giảm dần:
−2,9; −2,999; 2,9; 2,999.
Quảng cáo
Trả lời:
Lời giải:
Để sắp xếp các số thập phân sau theo thứ tự tăng dần (giảm dần), ta làm như sau:
Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.
Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:
- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.
- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.
a) Sắp xếp các số thập phân sau theo thứ tự tăng dần:
* Phân loại:
- Nhóm các số thập phân dương: 0,5; 2,4.
- Nhóm các số thập phân âm: −12,13; −2,4; −2,3.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương: ta so sánh phần nguyên của các số trên, vì 0 < 2 nên 0,5 < 2,4.
- Nhóm các số thập phân âm:
+ Số đối của các số −12,13; −2,4; −2,3 lần lượt là 12,13; 2,4; 2,3.
+ Số 12,13 có phần nguyên là 4;
+ Hai số 2,4; 2,3 đều có phần nguyên là 2 nên ta so sánh phần thập phân của hai số.
+ Số 2,4 và 2,3 có hàng phần mười lần lượt là 4 và 3. Vì 4 > 3 nên 2,4 > 2,3.
Do đó 12,13 > 2,4 > 2,3 hay −12,13 < −2,4 < −2,3.
Từ đó ta suy ra: −12,13 < −2,4 < −2,3 < 0,5 < 2,4.
Vậy các số được sắp xếp thứ tự tăng dần là: −12,13; −2,4; −2,3; 0,5; 2,4.
b) Sắp xếp các số thập phân sau theo thứ tự giảm dần:
* Phân loại:
- Nhóm các số thập phân dương: 2,9; 2,999.
- Nhóm các số thập phân âm: −2,9; −2,999.
* So sánh các số thập phân trong theo nhóm:
- Nhóm các số thập phân dương:
+ So sánh phần nguyên: cả hai số 2,9 và 2,999 đều có phần nguyên là 2.
+ So sánh phần thập phân: Hàng phần mười của hai số đều là 9.
Ta tiếp tục so sánh hàng phần trăm: chữ số hàng phần trăm của 2,9 và 2,999 lần lượt là 0 và 9. Vì 9 > 0 nên 2,999 > 2,9.
- Nhóm các số thập phân âm:
+ Số đối của các số −2,9; −2,999 lần lượt là 2,9; 2,999.
Ở phần trên ta đã chứng minh được 2,999 > 2,9 nên −2,999 < −2,9.
Từ đó ta suy ra: 2,999 > 2,9 > −2,9 > −2,999.
Vậy các số được sắp xếp thứ tự giảm dần là: 2,999; 2,9; −2,9; −2,999.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Để sắp xếp các số theo thứ tự giảm dần, ta thực hiện như sau:
Bước 1: Chia thành 2 nhóm: nhóm số dương và nhóm số âm (số dương luôn lớn hơn 0 và lớn hơn số âm)
- Nhóm số dương: 0,6;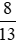 .
.
- Nhóm số âm: 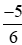 ;
; 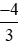 ; −1,75.
; −1,75.
Bước 2: Ta so sánh các số theo nhóm với nhau:
- Nhóm số dương: 0,6; 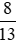 .
.
Ta có: 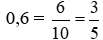 ;
;
Quy đồng hai phân số 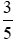 và
và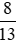 .
.
Mẫu số chung: 65.
Ta thực hiện: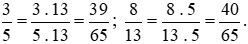
Vì 40 > 39 nên 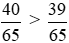 hay
hay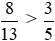
Do đó 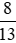 > 0,6.
> 0,6.
- Nhóm số âm: 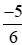 ;
;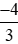 ; −1,75.
; −1,75.
Ta có: 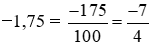 .
.
Quy đồng các phân số 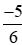 ;
; 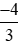 ;
; 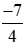 .
.
Mẫu số chung: 24.
Ta thực hiện: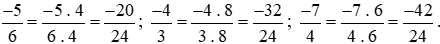
Vì −20 > −32 > −42 nên 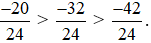
Hay 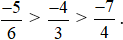
Do đó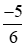 >
>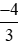 > −1,75.
> −1,75.
Từ đó suy ra 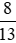 > 0,6 > 0 >
> 0,6 > 0 >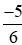 >
>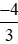 > −1,75.
> −1,75.
Vậy các số được sắp xếp theo thứ tự giảm dần là: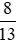 ; 0,6; 0;
; 0,6; 0;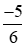 ;
;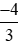 ; −1,75.
; −1,75.
Lời giải
Lời giải:
- Các phân số thập phân được viết dưới dạng số thập phân.
- Số các chữ số thập phân bằng đúng số các chữ số 0 ở mẫu của phân số thập phân.
Đổi lần lượt các số thập phân trên ra phân số thập phân, ta được:
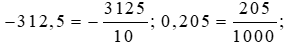
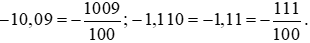
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
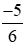 ;
;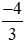 ; 0;
; 0; 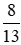 ; −1,75.
; −1,75.