Câu hỏi trong đề: Đề thi Giữa kì 1 Toán 8 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
A = 12 – x2– 6x
= –(x2+ 6x – 12)
= –(x2+ 6x + 9 – 21)
= –(x + 3)2+ 21
Có (x + 3)2≥ 0 
⇒ –(x + 3)2≤ 0 
⇒ –(x + 3)2+ 21 ≤ 21 
⇒ A ≤ 21
Dấu “=” xảy ra khi (x + 3)2= 0
⇔ x + 3 = 0
⇔ x = – 3
Vậy giá trị lớn nhất của A = 21 khi x = – 3.
Sách thầy cô Vietjack biên soạn
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
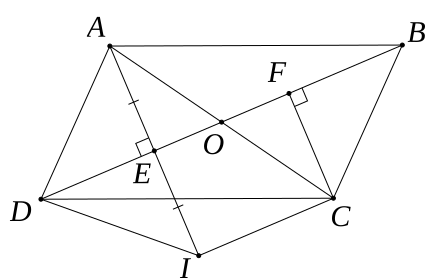
Cho hình bình hành ABCD (AD < AB), O là giao điểm hai đường chéo AC, BD. Gọi E, F lần lượt là hình chiếu của A và C trên BD.
a) Chứng minh tứ giác AECF là hình bình hành.
b) Gọi I là điểm đối xứng của A qua BD. Chúng minh EO là đường trung bình của tam giác AIC.
c) Chứng minh tứ giác CIDB là hình thang cân.
Xem đáp án »
12/07/2024
4,305
Câu 3:
Hình thang cân ABCD (AB//CD) có . Khẳng định nào dưới đây là đúng?
Xem đáp án »
24/03/2022
1,578
Câu 5:
Phân tích đa thức thành nhân tử:
a) 15xy + 20xy2;
b) 4x2– y2+ 4x + 1.
Xem đáp án »
12/07/2024
1,044
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
-
Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận