Cho hình chóp đều S.ABC cạnh đáy bằng 2a và cạnh bên bằng 3a. Gọi M là điểm thay đổi trên cạnh AB, (P) qua M và song song với SA, BC chia khối chóp S.ABC thành hai phần. Biết thiết diện của hình chóp S.ABC cắt bởi (P) là hình thoi. Tính thể tích phần chứa đỉnh A.
Cho hình chóp đều S.ABC cạnh đáy bằng 2a và cạnh bên bằng 3a. Gọi M là điểm thay đổi trên cạnh AB, (P) qua M và song song với SA, BC chia khối chóp S.ABC thành hai phần. Biết thiết diện của hình chóp S.ABC cắt bởi (P) là hình thoi. Tính thể tích phần chứa đỉnh A.
A.
B.
C.
D.
Quảng cáo
Trả lời:
Đáp án C
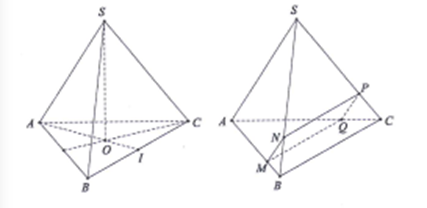
Gọi O là trọng tâm tam giác ABC, I là trung điểm BC.
Gọi N, P, Q lần lượt là giao điểm của (P) với các cạnh SB, SC, AC.
Tam giác ABC đều có cạnh bằng 2a
Vì SABC là hình chóp đều nên .
Xét tam giác vuông SOA có: .
Ta có: .
MNPQ là hình thoi .
Ta có: .
Đặt . Ta có công thức tính nhanh .
Áp dụng
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (đồng) là giá bán thực tế của mỗi kilôgam vải thiều .
Ta có thể lập luận như sau:
Giá 40 000 đồng thì bán được 30 kg vải thiều.
Giảm giá 4 000 đồng thì bán được thêm 40 kg vải thiều.
Giảm giá 40 000 – x thì bán được thêm bao nhiêu kg vải thiều?
Theo bài ra số kilôgam bán thêm được là: .
Do đó số kg vải thiều bán được tương ứng với giá bán x:
Gọi F(x) là hàm lợi nhuận thu được (F(x): đồng).
Ta có: .
Bài toán trở thành tìm giá trị lớn nhất của
trên [25000; 400000].
Ta có: .
Vì hàm F9x) liên tục trên đoạn [25000; 40000] nên ta có:
Vậy với x = 34000 thì F(x) đạt giá trị lớn nhất.
Vậy để cửa hàng đó thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi kg vải thiều là 34 000 đồng.
Lời giải
Đáp án B
Ta có điểm thuộc đường thẳng d, nên A(1; -3; 5) là giao điểm của d và D. Một vectơ chỉ phương của đường thẳng d là .
Ta xét
Nhận thấy , nên góc tạo bởi hai vectơ là góc nhọn tạo bởi d và D.
Ta có là vectơ chỉ phương của đường phân giác của góc nhọn tạo bởi d và D hay đường phân giác của góc nhọn tạo bởi d và D có vectơ chỉ phương là và đi qua điểm .
Do đó, phương trình phân giác cần tìm là hoặc .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. (-2; -1)
B. (-3; -1)
C.
D. (-2; 0)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 1083
B. 1380
C. 1830
D. 1038
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
D. 45 401 000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
