Câu hỏi:

04/05/2022 362

Gọi S là tổng các giá trị thực của m để phương trình $9 z^{2} + 6 z + 1 - m = 0$ có nghiệm phức thỏa mãn $|z| = 1$ . Tính S.

A.20

B.12

C.14

D.8

Xem lời giải

Câu hỏi trong đề: Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương trình $9 z^{2} + 6 z + 1 - m = 0 (*) c ó ∆' = 9 - 9 (1 - m) = 9 m$
Xét hai trường hợp sau:

Trường hợp 1. (*) có nghiệm thực $\Leftrightarrow ∆' \geq 0 \Leftrightarrow m \geq 0$ .

Khi đó, $|z| = 1 [z = 1 z = - 1]$

+) $z = 1 \Rightarrow m = 16$ (thỏa mãn).

+) $z = - 1 \Rightarrow m = 4$ (thỏa mãn).

Trường hợp 2. (*) có nghiệm phức $z = a + b i (b \neq 0) \Leftrightarrow ∆' < 0 \Leftrightarrow m < 0$ .

Nếu z là một nghiệm của phương trình $9 z^{2} + 6 z + 1 - m = 0$ thì $\vec{z}$ cũng là một nghiệm của phương trình $9 z^{2} + 6 z + 1 - m = 0$ .

Ta có $|z| = 1 \Leftrightarrow {|z|}^{2} = 1 \Leftrightarrow \frac{1 - m}{9} = 1 \Leftrightarrow m = - 8$ (thỏa mãn).

Vậy tổng các giá trị thực của m bằng 12.
Chọn B.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Người ta dự định xây dựng một tòa tháp 11 tầng tại một ngôi chùa nọ theo cấu trúc, diện tích của mặt sàn tầng trên bằng nửa diện tích mặt sàn tầng dưới, biết diện tích mặt đáy tháp là 15 m². Yêu cầu là nền tháp lát gạch hoa kích thước 30x30 (cm). Tính số lượng gạch hoa cần mua để lát sàn tháp.

A. 333 viên gạch.

B. 334 viên gạch.

C. 332 viên gạch.

D. 335 viên gạch.

Lời giải

Gọi $S_{1}$ là diện tích mặt đáy tháp. Ta có: $S 1 = 15 (m^{2})$ .

Theo yêu cầu khi xây dựng tòa tháp, diện tích mặt đáy các tầng tiếp theo là:
$S_{2} = \frac{1}{2} S_{1}$
$S_{3} = \frac{1}{2} S_{2} = {(\frac{1}{2})}^{2} S_{1}$

……
$S_{n} = {(\frac{1}{2})}^{n - 1} S_{1}$

Tổng diện tích mặt sàn 11 tầng tháp là $S = S_{1} + S 2 + . . . + S_{11} . (1 + \frac{1}{2} + \frac{1}{2^{2}} + . . . + \frac{1}{2^{10}}) = 15.1 . \frac{1 - \frac{1}{2^{11}}}{1 - \frac{1}{2}} \approx 29, 98 (m^{2})$

Diện tích mỗi viên gạch là $30.30 = 900 (c m^{2}) = 0, 09 (m^{2})$ .

Số lượng gạch hoa cần mua là

\frac{S}{0, 09} \approx 333, 17 (v i ê n)

(viên). Vậy cần mua 334 viên gạch.
Chọn B

Câu 2

Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số $y = |3 x^{4} - 4 x^{3} - 12 x^{2} + m|$ nghịch biến trên khoảng $(- \infty; - 1)$ ?

A. 4

B. 6

C. 3

D. 5

Lời giải

Chọn D

Xét hàm số $f (x) = 3 x^{4} - 4 x^{3} - 12 x^{2} + m \Rightarrow f^{'} (x) = 12 x^{3} - 12 x^{2} - 24 x$

Ta có $f^{'} (x) = 0 \Rightarrow [\begin{array}{l} x = - 1 \\ x = 0 \\ x = 2 \end{array}$

Bảng biến thiên

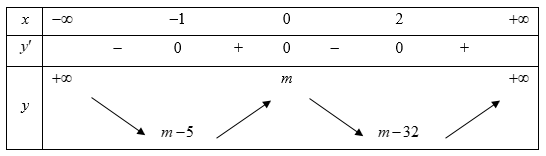
Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số (ảnh 1)

Hàm số $y = |f (x)|$ nghịch biến trên $(- \infty; - 1) \Leftrightarrow m - 5 \geq 0 \Leftrightarrow m \geq 5$

Do m là số nguyên nhỏ hơn 10 nên ta có $m \in \{5; 6; 7; 8; 9\}$ .

Vậy có 5 giá trị m thỏa mãn yêu cầu bài toán.

Câu 3

Gọi $(H)$ là tập hợp các điểm biểu diễn số phức z thỏa mãn $1 \leq |z - 1| \leq 2$ trong mặt phẳng phức. Khi đó, diện tích hình $(H)$ bằng

A. $2 π$

B. $3 π$

C. $4 π$

D. $5 π$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Thầy Thắng muốn sau 5 năm có 1 tỉ đồng để mua ôtô. Hỏi rằng thầy Thắng phải gửi ngân hàng mỗi tháng số tiền gần nhất với số tiền nào sau đây? Biết lãi suất hàng tháng là 0,5%, tiền lãi sinh ra hàng tháng được nhập vào tiền vốn, số tiền gửi hàng tháng là như nhau.

A. 14 261 000 đồng.

B. 14 260 500 đồng.

C. 14 260 000 đồng.

D. 14 261 500 đồng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Đồ thị hàm số $y = \frac{1 - 3 x}{x - 1}$ có tâm đối xứng là

I (- 1; - 3)

B. $I (- 1; 1)$

C. $I (- 3; 1)$

I (1; - 3)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2020 để phương trình $\log_{2} (m + \sqrt{m + 2^{x}}) = 2 x$ có nghiệm thực?

A. 2017

B. 2018

C. 2020

D. 2019

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hàm số $y = f (x)$ có đồ thị trên đoạn $[- 1; 4]$ như hình vẽ bên. Khi đó, tích phân $I = \int_{- 1}^{4} f (x) d x$ bằng bao nhiêu?

A. $I = 3$

B. $I = \frac{11}{2}$

I = 5

D. $I = \frac{5}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Gọi S là tổng các giá trị thực của m để phương trình 9z2+6z+1-m=0 có nghiệm phức thỏa mãn z=1 . Tính S.

Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số y=3x4 - 4x3 -12x2 + m nghịch biến trên khoảng (-∞;-1)?

Gọi (H) là tập hợp các điểm biểu diễn số phức z thỏa mãn 1≤z-1≤2 trong mặt phẳng phức. Khi đó, diện tích hình (H) bằng

Đồ thị hàm số y=1−3xx−1 có tâm đối xứng là

Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2020 để phương trình log2(m+m+2x)=2x có nghiệm thực?

Cho hàm số y=f(x) có đồ thị trên đoạn −1;4 như hình vẽ bên. Khi đó, tích phân I=∫−14f(x)dx bằng bao nhiêu?

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Gọi S là tổng các giá trị thực của m để phương trình $9 z^{2} + 6 z + 1 - m = 0$ có nghiệm phức thỏa mãn $|z| = 1$ . Tính S.

Có bao nhiêu giá trị nguyên của tham số m nhỏ hơn 10 để hàm số $y = |3 x^{4} - 4 x^{3} - 12 x^{2} + m|$ nghịch biến trên khoảng $(- \infty; - 1)$ ?

Gọi $(H)$ là tập hợp các điểm biểu diễn số phức z thỏa mãn $1 \leq |z - 1| \leq 2$ trong mặt phẳng phức. Khi đó, diện tích hình $(H)$ bằng

Đồ thị hàm số $y = \frac{1 - 3 x}{x - 1}$ có tâm đối xứng là

Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2020 để phương trình $\log_{2} (m + \sqrt{m + 2^{x}}) = 2 x$ có nghiệm thực?

Cho hàm số $y = f (x)$ có đồ thị trên đoạn $[- 1; 4]$ như hình vẽ bên. Khi đó, tích phân $I = \int_{- 1}^{4} f (x) d x$ bằng bao nhiêu?