Câu hỏi:

12/07/2024 1,799

Biểu đồ bên dưới thể hiện tỷ lệ phần trăm chi phí trong năm 2020 của một công ty.

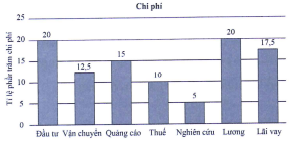
1. Tổng chi của công ty gấp bao nhiêu lần chi phí cho Nghiên cứu?

2. Nếu chi cho Quảng cáo là 210 triệu đồng thì chênh lệch giữa chi cho Vận chuyển và chi cho Thuế là bao nhiêu triệu đồng?

3. Nếu chi cho Lãi vay là 245 triệu đồng thì tổng chi cho Quảng cáo, Thuế và Nghiên cứu là bao nhiêu triệu đồng?

4. Năm 2020 công ty đã xây dựng tốt thương hiệu cũng như trả được thêm nhiều các khoản vay nên năm 2021 chi phí cho Lãi vay đã giảm 25% so với năm 2020 và công ty cũng quyết định giảm 20% chi phí cho Quảng cáo. Toàn bộ lượng giảm chi phí sẽ được dùng để tăng lương cho toàn bộ nhân viên. Hỏi chi phí cho Lương năm 2021 đã tăng bao nhiêu phần trăm so với năm 2020?

Xem lời giải

Câu hỏi trong đề: Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

1. Tổng chi của công ty gấp số lần chi phí cho Nghiên cứu là:

$\frac{20 + 12, 5 + 15 + 10 + 5 + 20 + 17, 5}{5} = 20$ (lần).

2. Chi phí cho Vận chuyển là: $\frac{210}{15} .12, 5 = 175$ (triệu đồng).

Chi phí cho Thuế là: $\frac{210}{15} .10 = 140$ (triệu đồng).

Chênh lệch giữa chi cho Vận chuyển và chi cho Thuế là: 175 – 140 = 35 (triệu đồng).

3. Tổng chi cho Quảng cáo, Thuế và Nghiên cứu là: $\frac{245}{17.5} . (15 + 10 + 5) = 420$ (triệu).

4. Gọi chi phí cho Quảng cáo năm 2020 là x. Khi đó:

+) Chi phí cho Lãi vay năm 2020 là: $\frac{x}{15} .17, 5 = \frac{7 x}{6}$ .

+) Chi phí cho Lương năm 2020 là: $\frac{x}{15} .20 = \frac{4 x}{3}$ .

Þ Chi phí cho Lương năm 2021 là: $\frac{4 x}{3} + 25 % . \frac{7 x}{6} + 20 % x = \frac{73 x}{40}$ .

Chi phí cho Lương năm 2021 đã tăng so với 2020 là:

$(\frac{73 x}{40} - \frac{4 x}{3}) : \frac{4 x}{3} = \frac{59}{160} = 36, 875 %$ .

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một cửa hàng bán quả vải thiều của Bắc Giang với giá bán mỗi kg là 40 000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 30 kg. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi kg 4000 đồng thì số vải thiều bán được tăng thêm là 40 kg. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi kilôgam là 25 000 đồng.

Xem đáp án

Lời giải

Gọi x (đồng) là giá bán thực tế của mỗi kilôgam vải thiều $(25000 \leq x \leq 40000)$ .

Ta có thể lập luận như sau:

Giá 40 000 đồng thì bán được 30 kg vải thiều.

Giảm giá 4 000 đồng thì bán được thêm 40 kg vải thiều.

Giảm giá 40 000 – x thì bán được thêm bao nhiêu kg vải thiều?

Theo bài ra số kilôgam bán thêm được là: $(40000 - x) . \frac{40}{4000} = \frac{1}{100} (40000 - x)$ .

Do đó số kg vải thiều bán được tương ứng với giá bán x:

$30 + \frac{1}{100} (40000 - x) = - \frac{1}{100} x + 430$

Gọi F(x) là hàm lợi nhuận thu được (F(x): đồng).

Ta có: $F (x) = (- \frac{1}{100} x + 430) . (x - 25000) = - \frac{1}{100} x^{2} + 680 x - 10750000$ .

Bài toán trở thành tìm giá trị lớn nhất của

$F (x) = - \frac{1}{100} x^{2} + 680 x - 10750000$ trên [25000; 400000].

Ta có: $F^{'} (x) = - \frac{1}{50} x + 680$ . $F^{'} (x) = 0 \Leftrightarrow - \frac{1}{50} x + 680 = 0 \Leftrightarrow x = 34000$

Vì hàm F9x) liên tục trên đoạn [25000; 40000] nên ta có:

$F (25000) = 0, F (34000) = 810000, F (40000) = 450000$

Vậy với x = 34000 thì F(x) đạt giá trị lớn nhất.

Vậy để cửa hàng đó thu được lợi nhuận lớn nhất thì giá bán thực tế của mỗi kg vải thiều là 34 000 đồng.

Câu 2

Trong không gian Oxyz, cho đường thẳng $d : \{\begin{cases} x = 1 + 3 t \\ y = - 3 \\ z = 5 + 4 t \end{cases}$ . Gọi $Δ$ là đường thẳng đi qua điểm A(1; -3; 5) và có vectơ chỉ phương $\vec{u} (1; 2; - 2)$ . Đường phân giác của góc nhọn tạo bởi d và $Δ$ có phương trình là

A. $\{\begin{cases} x = - 1 + 2 t \\ y = 2 - 5 t \\ z = 6 + 11 t \end{cases}$

B. $\{\begin{cases} x = - 1 + 2 t \\ y = 2 - 5 t \\ z = - 6 + 11 t \end{cases}$

C. $\{\begin{cases} x = 1 + 7 t \\ y = - 3 + 5 t \\ z = 5 + t \end{cases}$

D. $\{\begin{cases} x = 1 - t \\ y = - 3 \\ z = 5 + 7 t \end{cases}$

Lời giải

Đáp án B

Ta có điểm $A (1; - 3; 5)$ thuộc đường thẳng d, nên A(1; -3; 5) là giao điểm của d và D. Một vectơ chỉ phương của đường thẳng d là $\vec{v} (- 3; 0; - 4)$ .

Ta xét

$\vec{u_{1}} = \frac{1}{|\vec{u}|} . \vec{u} = \frac{1}{3} (1; 2; - 2) = (\frac{1}{3}; \frac{2}{3}; - \frac{2}{3}); \vec{v_{1}} = \frac{1}{|\vec{v}|} . \vec{v} = \frac{1}{5} (- 3; 0; - 4) = (- \frac{3}{5}; 0; - \frac{4}{5})$

Nhận thấy $\vec{u_{1}} . \vec{v_{1}} > 0$ , nên góc tạo bởi hai vectơ $\vec{u_{1}}, \vec{v_{1}}$ là góc nhọn tạo bởi d và D.

Ta có $\vec{w} = \vec{u_{1}} + \vec{v_{1}} = (- \frac{4}{15}; \frac{10}{15}; - \frac{22}{15}) = - \frac{2}{15} (2; - 5; 11)$ là vectơ chỉ phương của đường phân giác của góc nhọn tạo bởi d và D hay đường phân giác của góc nhọn tạo bởi d và D có vectơ chỉ phương là $\vec{w_{1}} = (2; - 5; 11)$ và đi qua điểm $A (1; - 3; 5)$ .

Do đó, phương trình phân giác cần tìm là $\{\begin{cases} x = 1 + 2 t \\ y = - 3 - 5 t \\ z = 5 + 11 t \end{cases}$ hoặc $\{\begin{cases} x = - 1 + 2 t \\ y = 2 - 5 t \\ z = - 6 + 11 t \end{cases}$ .

Câu 3

Cho tứ diện đều ABCD có cạnh bằng $\sqrt{11}$ . Gọi I là trung điểm cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

A. 2

B. $2 \sqrt{2}$

C. $3 \sqrt{2}$

D. $\sqrt{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Người ta muốn làm giá đỡ cho quả cầu bằng ngọc có bán kính r sao cho phần quả cầu bị khuất chiếm $\frac{1}{6}$ quả cầu theo chiều cao của nó. Biết giá đỡ hình trụ và rỗng phía trong, tính bán kính mặt trong của giá đỡ.

A. $\frac{\sqrt{5}}{3} r$

B. $\frac{1}{3} r$

C. $\frac{2 \sqrt{2}}{3} r$

D. $\frac{2}{3} r$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một cấp số cộng có $u_{7} = 27$ và $u_{20} = 79$ . Tổng của 30 số hạng đầu của cấp số cộng này là

A. 1083

B. 1380

C. 1830

D. 1038

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số $y = f (x)$ liên tục và xác định trên $ℝ$ , biết rằng $f^{'} (x + 2) = x^{2} - 3 x + 2$ . Hàm số $y = f (x^{2} + 4 x + 7)$ đồng biến trên khoảng nào dưới đây?

A. (-2; -1)

B. (-3; -1)

C. $(1; + \infty)$

D. (-2; 0)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một anh sinh viên T nhập học đại học vào tháng 8 năm 2020. Bắt đầu từ tháng 9 năm 2020, cứ vào ngày mồng một hàng tháng anh vay ngân hàng 3 triệu đồng với lãi suất cố định 0,8%/tháng. Lãi tháng trước được cộng vào số nợ để tiếp tục tính lãi cho tháng tiếp theo. Vào ngày mồng một hàng tháng kể từ tháng 9 năm 2022 về sau anh không vay ngân hàng nữa và anh còn trả được cho ngân hàng 2 triệu đồng do việc làm thêm. Hỏi ngay sau ngày anh ra trường (30/6/2024) anh còn nợ ngân hàng bao nhiêu tiền?

A. 49 024 000 đồng.

B. 46 640 000 đồng.

C. 47 024 000 đồng.

D. 45 401 000 đồng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Trong không gian Oxyz, cho đường thẳng d:x=1+3ty=−3z=5+4t. Gọi Δ là đường thẳng đi qua điểm A(1; -3; 5) và có vectơ chỉ phương u→1;2;−2. Đường phân giác của góc nhọn tạo bởi d và Δ có phương trình là

Cho tứ diện đều ABCD có cạnh bằng 11. Gọi I là trung điểm cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

Người ta muốn làm giá đỡ cho quả cầu bằng ngọc có bán kính r sao cho phần quả cầu bị khuất chiếm 16 quả cầu theo chiều cao của nó. Biết giá đỡ hình trụ và rỗng phía trong, tính bán kính mặt trong của giá đỡ.

Một cấp số cộng có u7=27 và u20=79. Tổng của 30 số hạng đầu của cấp số cộng này là

Cho hàm số y=fx liên tục và xác định trên ℝ, biết rằng f'x+2=x2−3x+2. Hàm số y=fx2+4x+7 đồng biến trên khoảng nào dưới đây?

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tứ diện đều ABCD có cạnh bằng $\sqrt{11}$ . Gọi I là trung điểm cạnh CD. Tính khoảng cách giữa hai đường thẳng AC và BI.

Người ta muốn làm giá đỡ cho quả cầu bằng ngọc có bán kính r sao cho phần quả cầu bị khuất chiếm $\frac{1}{6}$ quả cầu theo chiều cao của nó. Biết giá đỡ hình trụ và rỗng phía trong, tính bán kính mặt trong của giá đỡ.

Một cấp số cộng có $u_{7} = 27$ và $u_{20} = 79$ . Tổng của 30 số hạng đầu của cấp số cộng này là

Cho hàm số $y = f (x)$ liên tục và xác định trên $ℝ$ , biết rằng $f^{'} (x + 2) = x^{2} - 3 x + 2$ . Hàm số $y = f (x^{2} + 4 x + 7)$ đồng biến trên khoảng nào dưới đây?