Cho hình lăng trụ đứng ABCD.A'B'C'D' với đáy là hình thoi có cạnh bằng AA' = 6a, BCD^=120°. Gọi M, N, K lần lượt là trung điểm của AB', B'C, BD'. Tính thể tích khối đa diện lồi có các đỉnh là các điể...

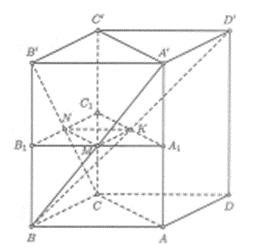
Đáp án C Gọi V là thể tích của khối lăng trụ ABCD.A'B'C'D'. Gọi A1, B1, C1 lần lượt là giao điểm của AA', BB', CC' và mặt phẳng (MNK). Thể tích của khối lăng trụ ABC.A1B1C1 là: VABC.A1B1C1=14VABCD.A'B'C'D'=14V. Gọi V1, V2, V3 lần lượt là thể tích của khối tứ diện AA1MK, BB1MN, CC1NK. Ta có +) V1=VA.A1MK=13.SΔA1MK.AA1=13.14SΔA1B1C1.AA1 =112VABC.A1B1C1=112.14V=148 +) V2=VB.B1MN=13.SΔB1MN.BB1=13.14SΔB1A1C1.BB1 =112VABC.A1B1C1=112.14V=148 +) V3=VC.C1NK=13.SΔC1NK.CC1=13.14SΔC1B1A1.CC1 =112VABC.A1B1C1=112.14V=148 +) V=SABCD.A'A=2SΔBCD.A'A=2.12.4a.4a.sin120°.6a=48a33 Do đó, thể tích khối đa diện lồi ABCMNK là VABCMNK=14VABCD.A'B'C'D'−V1+V2+V3=14V−3.148V=316V=316.48a33=9a33 Vậy VABCMNK=9a33.

Câu hỏi:

04/05/2022 1,345

Cho hình lăng trụ đứng ABCD.A'B'C'D' với đáy là hình thoi có cạnh bằng AA' = 6a, $\hat{B C D} = 120 °$ . Gọi M, N, K lần lượt là trung điểm của AB', B'C, BD'. Tính thể tích khối đa diện lồi có các đỉnh là các điểm A, B, C, M, N, K.

A. $9 a^{3}$

B. $16 a^{3} \sqrt{3}$

C. $9 a^{3} \sqrt{3}$

D. $12 a^{3} \sqrt{3}$

Xem lời giải

Câu hỏi trong đề: Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án C

Cho hình lăng trụ đứng ABCD.A'B'C'D' với đáy là hình thoi có cạnh bằng 4a (ảnh 1)

Gọi V là thể tích của khối lăng trụ $A B C D . A^{'} B^{'} C^{'} D^{'}$ .

Gọi A₁, B₁, C₁ lần lượt là giao điểm của AA', BB', CC' và mặt phẳng (MNK).

Thể tích của khối lăng trụ ABC.A₁B₁C₁ là:

$V_{A B C . A_{1} B_{1} C_{1}} = \frac{1}{4} V_{A B C D . A^{'} B^{'} C^{'} D^{'}} = \frac{1}{4} V$ .

Gọi V₁, V₂, V₃ lần lượt là thể tích của khối tứ diện AA₁MK, BB₁MN, CC₁NK. Ta có

+) $V_{1} = V_{A . A_{1} M K} = \frac{1}{3} . S_{Δ A_{1} M K} . A A_{1} = \frac{1}{3} . \frac{1}{4} S_{Δ A_{1} B_{1} C_{1}} . A A_{1}$

$= \frac{1}{12} V_{A B C . A_{1} B_{1} C_{1}} = \frac{1}{12} . \frac{1}{4} V = \frac{1}{48}$

+) $V_{2} = V_{B . B_{1} M N} = \frac{1}{3} . S_{Δ B_{1} M N} . B B_{1} = \frac{1}{3} . \frac{1}{4} S_{Δ B_{1} A_{1} C_{1}} . B B_{1}$

$= \frac{1}{12} V_{A B C . A_{1} B_{1} C_{1}} = \frac{1}{12} . \frac{1}{4} V = \frac{1}{48}$

+) $V_{3} = V_{C . C_{1} N K} = \frac{1}{3} . S_{Δ C_{1} N K} . C C_{1} = \frac{1}{3} . \frac{1}{4} S_{Δ C_{1} B_{1} A_{1}} . C C_{1}$

$= \frac{1}{12} V_{A B C . A_{1} B_{1} C_{1}} = \frac{1}{12} . \frac{1}{4} V = \frac{1}{48}$

+) $V = S_{A B C D} . A^{'} A = 2 S_{Δ B C D} . A^{'} A = 2. \frac{1}{2} . (4 a) . (4 a) . \sin 120 ° . (6 a) = 48 a^{3} \sqrt{3}$

Do đó, thể tích khối đa diện lồi ABCMNK là

$V_{A B C M N K} = \frac{1}{4} V_{A B C D . A^{'} B^{'} C^{'} D^{'}} - (V_{1} + V_{2} + V_{3}) = \frac{1}{4} V - 3. \frac{1}{48} V = \frac{3}{16} V = \frac{3}{16} .48 a^{3} \sqrt{3} = 9 a^{3} \sqrt{3}$

Vậy $V_{A B C M N K} = 9 a^{3} \sqrt{3}$ .

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình, giáo viên muốn thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.

A. $\frac{36}{285}$

B. $\frac{18}{285}$

C. $\frac{72}{285}$

D. $\frac{144}{285}$

Lời giải

Đáp án A

Ta có số phần tử của không gian mẫu là: $n (Ω) = C_{12}^{3} C_{9}^{3} C_{6}^{3} C_{3}^{3}$ . Để nhóm nào cũng có học sinh giỏi và học sinh khá thì:

- Chọn 2 học sinh giỏi và xếp vào 1 trong 4 nhóm: $C_{5}^{2} . C_{4}^{1}$ .

- Xếp 3 học sinh giỏi còn lại vào 3 nhóm còn lại: 3!.

- Xếp 4 học sinh khá vào 4 nhóm: 4!.

- Xếp 3 học sinh trung bình: 3!.

$\Rightarrow n (A) = C_{5}^{2} . C_{4}^{1} .3! .4! .3! \Rightarrow P (A) = \frac{36}{385}$ .

Câu 2

Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc xây dựng như đấu trường La Mã, tòa nhà Ellipse Tower Hà Nội, sử dụng trong thiết kế logo quảng cáo, thiết bị nội thất,... Xét một Lavabo làm bằng sứ đặc hình dạng là một nửa khối elip tròn xoay có thông số kĩ thuật mặt trên của Lavabo dài x rộng là 660 x 380 mm. Biết rằng Lavabo có độ dày đều là 20 mm.

A. 18,66dm³

B. 18,76dm³

C. 18,86dm³

D. 18,96dm³

Lời giải

Đáp án B

Rìa trong của Lavabo là một elip có bán trục lớn $a = \frac{660}{2} - 20 = 310 m m = 3, 1 d m$ , bán trục nhỏ $a = \frac{380}{2} - 20 = 170 m m = 1, 7 d m$ .

Áp dụng công thức tính nhanh thể tích khi qua elip quanh trục lớn, ta có $V = \frac{1}{2} . \frac{4}{3} π a b^{2} \approx 18, 76 d m^{3}$

Câu 3

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, SA vuông góc với mặt phẳng đáy và $A B = \sqrt{3} a$ . Gọi M là trung điểm BC. Khoảng cách giữa hai đường thẳng AC và SM bằng

A. $\frac{\sqrt{39} a}{12}$

B. $\frac{\sqrt{2} a}{3}$

C. $\frac{\sqrt{39} a}{13}$

D. $\frac{\sqrt{2} a}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Chia 150 cái kẹo giống nhau cho 5 người sao cho ai cũng có kẹo. Tính xác suất để mỗi người có ít nhất 10 cái kẹo (Làm tròn tới số thập phân thứ ba).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tập đoàn X có 6 công ty A, B, C, D, E, F. Trong năm 2020, tỷ lệ doanh thu của các công ty này được biểu thị như biểu đồ (hình bên).

1. Nếu doanh thu của công ty D là 650 tỷ đồng thì tổng doanh thu của công ty B và C là bao nhiêu tỷ đồng?

2. Doanh thu của công ty F nhiều hơn doanh thu của công ty D, C bao nhiêu phần trăm?

3. Nếu doanh thu của công ty E tăng 15% vào năm 2021 và doanh thu của các công ty khác không thay đổi thì tổng doanh thu của tập đoàn X tăng bao nhiêu phần trăm?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc $v_{1} (t) = 2 t$ (m/s). Đi được 12 giây, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc $a = - 12 (m / s^{2})$ . Tính quãng đường s(m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Năm 2020, một doanh nghiệp X có tổng doanh thu là 150 tỉ đồng. Dự kiến trong 10 năm tiếp theo, tổng doanh thu mỗi năm sẽ tăng thêm 12% so với năm liền trước. Theo dự kiến đó thì kể từ năm nào, tổng doanh thu của doanh nghiệp X vượt quá 360 tỉ đồng?

A. 2026.

B. 2027.

C. 2028.

D. 2029.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình lăng trụ đứng ABCD.A'B'C'D' với đáy là hình thoi có cạnh bằng AA' = 6a, BCD^=120°. Gọi M, N, K lần lượt là trung điểm của AB', B'C, BD'. Tính thể tích khối đa diện lồi có các đỉnh là các điểm A, B, C, M, N, K.

Bình luận

Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá, 3 học sinh trung bình, giáo viên muốn thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Tính xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá.

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, SA vuông góc với mặt phẳng đáy và AB=3a. Gọi M là trung điểm BC. Khoảng cách giữa hai đường thẳng AC và SM bằng

Chia 150 cái kẹo giống nhau cho 5 người sao cho ai cũng có kẹo. Tính xác suất để mỗi người có ít nhất 10 cái kẹo (Làm tròn tới số thập phân thứ ba).

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình lăng trụ đứng ABCD.A'B'C'D' với đáy là hình thoi có cạnh bằng AA' = 6a, $\hat{B C D} = 120 °$ . Gọi M, N, K lần lượt là trung điểm của AB', B'C, BD'. Tính thể tích khối đa diện lồi có các đỉnh là các điểm A, B, C, M, N, K.

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = a, SA vuông góc với mặt phẳng đáy và $A B = \sqrt{3} a$ . Gọi M là trung điểm BC. Khoảng cách giữa hai đường thẳng AC và SM bằng