Câu hỏi:

05/05/2022 541

Cho tứ diện đều ABCD cạnh a. Lấy N, M lần lượt là trung điểm AB và AC. Tính khoảng cách d giữa CN và DM.

A. $d = a \sqrt{\frac{3}{2}}$

B. $d = \frac{a \sqrt{10}}{10}$

C. $d = \frac{a \sqrt{3}}{2}$

D. $d = \frac{a \sqrt{70}}{35}$

Xem lời giải

Câu hỏi trong đề: Bộ 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án D

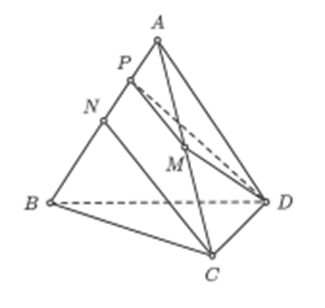
Cho tứ diện đều ABCD cạnh a. Lấy N, M lần lượt là trung điểm AB và AC. Tính (ảnh 1)

+) Gọi P là trung điểm đọan AN.

Ta có $\{\begin{cases} C N / / P M \\ P M \subset (D M P) \end{cases} \Rightarrow C N / / (D M P)$ .

Suy ra $d (C N, D M) = d (C N, (D M P)) = d (N, (D M P))$

$= d (A, (D M P))$ .

+) Khi đó $\frac{V_{A . D M P}}{V_{A . B C D}} = \frac{A P}{A B} . \frac{A M}{A C} . \frac{A D}{A D} = \frac{1}{8}$ , mà tứ diện ABCD đều nên $V_{A . B C D} = \frac{a^{3} \sqrt{2}}{12}$

$\Rightarrow V_{A . D M P} = \frac{a^{3} \sqrt{2}}{96} \Rightarrow \frac{1}{3} d (A, (D M P)) . S_{Δ D M P} = \frac{a^{3} \sqrt{2}}{96}$ .

+) Lại có tam giác ABC đều nên $D M = \frac{a \sqrt{3}}{2}$ , $C N = \frac{a \sqrt{3}}{2} \Rightarrow M P = \frac{a \sqrt{3}}{4}$ đều nên.

Xét tam giác DPA có $D P^{2} = A D^{2} + A P^{2} - 2 A D . A P . \cos \hat{P A D} = a^{2} + {(\frac{a}{4})}^{2} - 2. a . \frac{a}{4} . \cos 60 ° = \frac{13 a^{2}}{16}$

$\Rightarrow D P = \frac{a \sqrt{13}}{4}$ .

Nửa chu vi tam giác DMP là: $p = \frac{\frac{a \sqrt{3}}{2} + \frac{a \sqrt{3}}{4} + \frac{a \sqrt{13}}{4}}{2} = \frac{a (\sqrt{13} + 3 \sqrt{3})}{8}$

$\Rightarrow S_{Δ D M P} = \sqrt{p (p - D M) (p - M P) (p - D P)} = \frac{a^{2} \sqrt{35}}{32}$ .

Vậy $d (A, (D M P)) = \frac{\frac{a^{3} \sqrt{2}}{96}}{\frac{1}{3} . \frac{a^{2} \sqrt{35}}{32}} = \frac{a \sqrt{70}}{35} \Rightarrow d (C N, D M) = \frac{a \sqrt{70}}{35}$ .

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD biết A(1; 0; 1), B(1; 0 -3) và điểm D có hoành độ âm. Mặt phẳng (ABCD) đi qua gốc tọa độ O. Khi đó đường thẳng d là trục đường tròn ngoại tiếp hình vuông ABCD có phương trình

A. $d : \{\begin{cases} x = - 1 \\ y = t \\ z = - 1 \end{cases}$

B. $d : \{\begin{cases} x = 1 \\ y = t \\ z = - 1 \end{cases}$

C. $d : \{\begin{cases} x = - 1 \\ y = t \\ z = 1 \end{cases}$

D. $d : \{\begin{cases} x = t \\ y = 1 \\ z = t \end{cases}$

Lời giải

Đáp án A

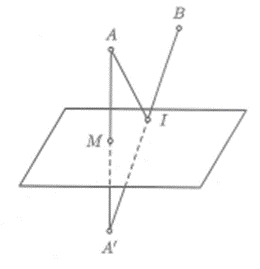
Trong không gian với hệ tọa độ Oxyz, cho hình vuông ABCD biết A(1; 0; 1), B(1; 0 -3), (ảnh 1)

Ta có $\vec{A B} = (0; 0; - 4) = - 4 (0; 0; 1)$ . Hay AB có vectơ chỉ phương $\vec{k} = (0; 0; 1)$ .

Mặt phẳng (ABCD) có một vectơ pháp tuyến $[\vec{O A}; \vec{O B}] = (0; 4; 0) = 4 (0; 1; 0)$ , hay $\vec{j} = (0; 1; 0)$ là một vectơ pháp tuyến của mặt phẳng (ABCD).

Vì $\{\begin{cases} A D ⊥ A B \\ A D \subset (A B C D) \end{cases}$ nên $\{\begin{cases} \vec{A D} ⊥ \vec{k} \\ \vec{A D} ⊥ \vec{j} \end{cases}$ .

Đường thẳng AD có vectơ chỉ phương là $[\vec{j}; \vec{k}] = (1; 0; 0)$ .

Phương trình đường thẳng AD là: $\{\begin{cases} x = 1 + t \\ y = 0 \\ z = 1 \end{cases}$ . Do đó $D (1 + t; 0; 1)$ .

Mặt khác $A D = A B \Leftrightarrow \sqrt{t^{2} + 0^{2} + {(1 - 1)}^{2}} = 4 \Leftrightarrow [\begin{array}{l} t = 4 \\ t = - 4 \end{array}$ .

Vì điểm D có hoành độ âm nên D(-3; 0; 1).

Vì tâm I của hình vuông ABCD là trung điểm BD nên I = (-1; 0; -1).

Đường thẳng d là trục đường tròn ngoại tiếp hình vuông ABCD có vectơ pháp tuyến là $\vec{j} = (0; 1; 0)$ , nên phương trình đường thẳng d là: $d : \{\begin{cases} x = - 1 \\ y = t \\ z = - 1 \end{cases}$ .

Câu 2

Cho hàm số $y = \{\begin{cases} x^{2} + a x + b khi x \geq 2 \\ x^{3} - x^{2} - 8 x + 10 khi x < 2 \end{cases}$ , biết hàm số có đạo hàm tại điểm x = 2. Giá trị của ab bằng

A. 2

B. 4

C. 1

D. -8

Lời giải

Đáp án D

Để hàm số có đạo hàm tại x = 2 thì hàm số phải liên tục tại x = 2.

Do đó $\lim_{x \to 2^{-}} (x^{3} - x^{2} - 8 x + 10) = \lim_{x \to 2^{+}} (x^{2} + a x + b) \Leftrightarrow - 2 = 4 + 2 a + b \Leftrightarrow 2 a + b = - 6$ .

Hàm số có đạo hàm tại điểm x = 2 nên

$\lim_{x \to 2^{-}} \frac{f (x) - f (2)}{x - 2} = \lim_{x \to 2^{+}} \frac{f (x) - f (2)}{x - 2} \Leftrightarrow \lim_{x \to 2^{-}} \frac{x^{3} - x^{2} - 8 x + 10 - (- 2)}{x - 2} = \lim_{x \to 2 +} \frac{x^{2} + a x + b - (4 + 2 a + b)}{x - 2} \Leftrightarrow \lim_{x \to 2^{-}} (x^{2} + x - 6) = \lim_{x \to 2^{+}} (x + 2 + a) \Leftrightarrow 4 + a = 0 \Leftrightarrow a = - 4$

Suy ra b = 2. Vậy ab = -8.

Câu 3

Bạn An muốn mua tặng mẹ một món quà trị giá 1 025 000đ. Để tạo sự bất ngờ cho mẹ, bạn bí mật thực hiện kế hoạch nuôi heo đất từ số tiền tiêu vặt hàng ngày của mình như sau: Ngày đầu tiên bạn bỏ vào heo đất 5000đ, các ngày tiếp theo, mỗi ngày bạn bỏ vào heo đất nhiều hơn ngày trước đó 1000đ. Hỏi bạn An phải thực hiện kế hoạch trong bao nhiêu ngày thì có đủ tiền mua quà tặng mẹ?

A. 39 ngày.

B. 40 ngày.

C. 41 ngày.

D. 50 ngày.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 1, AD = AA' = 2. Bán kính mặt cầu ngoại tiếp hình tứ diện AB'CD' bằng

A. $\sqrt{5}$

B. 3

C. $\frac{3}{2}$

D. $\frac{\sqrt{5}}{2}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Có bao nhiêu giá trị nguyên dương của m để bất phương trình $m {.16}^{x} - (2 m + 1) {.12}^{x} + m {.9}^{x} \leq 0$ nghiệm đúng với mọi $x \in (0; 1)$ ?

A. 6

B. 11

C. 12

D. 13

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng

A. $\frac{37}{12}$

B. $\frac{7}{12}$

C. $\frac{11}{12}$

D. $\frac{5}{12}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một nguồn đặt tại điểm O phát ra âm đẳng hướng. Mức cường độ âm tại điểm M cách O một khoảng R được tính bởi công thức $L_{M} = \log \frac{k}{R^{2}} (B)$ , với k > 0 là hằng số. Biết điểm O thuộc đoạn thẳng AB và mức cường độ âm tại A và B lần lượt là $L_{A} = 4, 3 (B)$ và $L_{B} = 5 (B)$ . Mức cường độ âm tại trung điểm của AB bằng

A. 4,65

B. 4,58

C. 5,42

D. 9,40

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho hàm số $y = \{\begin{cases} x^{2} + a x + b khi x \geq 2 \\ x^{3} - x^{2} - 8 x + 10 khi x < 2 \end{cases}$ , biết hàm số có đạo hàm tại điểm x = 2. Giá trị của ab bằng

Có bao nhiêu giá trị nguyên dương của m để bất phương trình $m {.16}^{x} - (2 m + 1) {.12}^{x} + m {.9}^{x} \leq 0$ nghiệm đúng với mọi $x \in (0; 1)$ ?