Câu hỏi:

06/05/2022 5,128

Cho một tấm tôn hình vuông có cạnh bằng a. Người ta cắt 4 góc của tấm tôn để được một tấm tôn mới như hình vẽ.

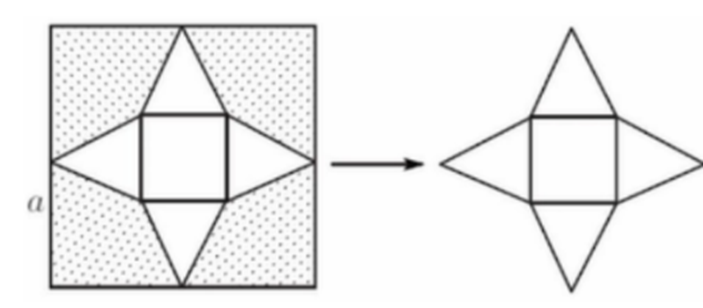
Từ tấm tôn mới, người ta gặp được một hình chóp tứ giác đều. Để khối chóp thu được có thể tích lớn nhất thì diện tích các miếng tốn bỏ đi là

A. $\frac{a^{3}}{3}$

B. $\frac{3 a^{2}}{5}$

C. $\frac{a^{2}}{\sqrt{5}}$

D. $\frac{2 a^{2}}{5}$

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá tư duy Đọc hiểu, Toán học - ĐH Bách khoa năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp giải:

Gọi x là độ dài của cạnh đáy của khối chóp

hh là chiều cao của khối chóp, h′ là chiều cao của tam giác cân ở mặt bên của khối chóp.

Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x

Bước 2: Tìm max của $f (x) = - 2 a x^{5} + a^{2} x^{4}$ với x>0

$V_{\max} \Leftrightarrow f {(x)}_{\max}$

Bước 3: Tìm phần diện tích bị bỏ

Giải chi tiết:

Gọi x là độ dài của cạnh đáy của khối chóp

h là chiều cao của khối chóp, h′ là chiều cao của tam giác cân ở mặt bên của khối chóp.

Bước 1: Biểu diễn h và thể tích V của khối chóp theo a và x

Ta có: $x + 2 h^{'} = a \Rightarrow h^{'} = \frac{a - x}{2}$

Ta có: $h^{2} + {(\frac{x}{2})}^{2} = {(\frac{a - x}{2})}^{2} \Leftrightarrow h = \sqrt{{(\frac{a - x}{2})}^{2} - {(\frac{x}{2})}^{2}} = \frac{\sqrt{a^{2} - 2 a x}}{2}$

Thể tích khối chóp: $V = \frac{1}{3} \cdot \frac{\sqrt{a^{2} - 2 a x}}{2} \cdot x^{2} = \frac{1}{6} \sqrt{- 2 a x^{5} + a^{2} x^{4}}$

Bước 2: Tìm max của $f (x) = - 2 a x^{5} + a^{2} x^{4}$ với x > 0.

Xét hàm số $f (x) = - 2 a x^{5} + a^{2} x^{4}$ với x > 0

$V_{\max} \Leftrightarrow f {(x)}_{\max}$

Ta có: $f^{'} (x) = - 10 a x^{4} + 4 a^{2} x^{3}, f^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \frac{2 a}{5} \end{array}$

$\Rightarrow \max f (x) = f (\frac{2 a}{5}) = \frac{16 a^{6}}{3125}$

Dấu "=" xảy ra khi và chỉ khi $x = \frac{2 a}{5}$

Bước 3: Tìm phần diện tích bị bỏ $\Rightarrow S = x^{2} + 4 \cdot \frac{1}{2} . x . \frac{a - x}{2} = \frac{2 a^{2}}{5}$

Vậy diện tích bị bỏ là $\frac{3 a^{2}}{5}$ .

Chọn B

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S ABC có SA ^ ( ABC ), tam giác ABC vuông tại B , SA = BC = a , AC = 2 a. Khoảng cách từ điểm A đến mặt phẳng (SBC) là

A. a

B. $\sqrt{2} a$

C. $a \sqrt{3}$

D. $\frac{a \sqrt{3}}{2}$

Lời giải

Phương pháp giải:

Bước 1: Kẻ AH vuông góc với SB. Chứng minh AH⊥(SBC)

Bước 2: Tính AH

Giải chi tiết:

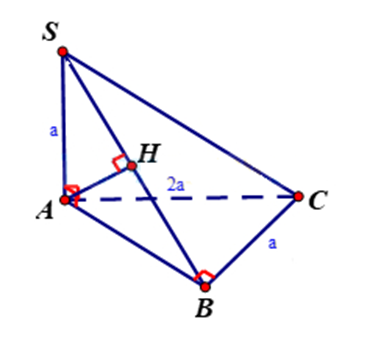
: Cho hình chóp S ABC có SA   ABC , tam giác ABC vuông tại B , SA = BC = a , AC  2 a. Khoảng cách từ điểm A đến mặt phẳng (SBC) (ảnh 1)

Bước 1: Kẻ AH vuông góc với SB. Chứng minh $A H = d (A, (S B C))$

Kẻ AH vuông góc với SB.

Ta có:

$\{\begin{cases} SA ⊥ (A B C) \Rightarrow S A ⊥ B C \\ B C ⊥ A B \end{cases} \Rightarrow B C ⊥ (S A B) = > B C ⊥ A H$

Lại có $A H ⊥ S B = > A H ⊥ (S B C) \Rightarrow A H = d (A, (S B C))$

Bước 2: Tính AH

Xét tam giác vuông ABC có: $A B = \sqrt{A C^{2} - B C^{2}} = a \sqrt{3}$

Xét tam giác vuông SAB có: $\frac{1}{A H^{2}} = \frac{1}{S A^{2}} + \frac{1}{A B^{2}} = \frac{1}{a^{2}} + \frac{1}{3 a^{2}} = \frac{4}{3 a^{2}} = > A H = \frac{a \sqrt{3}}{2}$

Chọn D

Câu 2

Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó chia hết cho 3.

A. 180

B. 162

C. 210

D. 30

Lời giải

Chọn A

Phương pháp giải:

Bước 1: Gọi số cần tìm là $\bar{a b c}$

Tách các bộ số chia hết cho 3, chia 3 dư 1 và chia 3 dư 2.

Bước 2: Xét các trường hợp bộ số chia hết cho 3

+) a, b, c đều chia hết cho 3 $\Rightarrow a, b, c = {3; 6; 9}$

+) $a, b, c \equiv 1 (\mod 3) \Rightarrow a, b, c \in \{1; 4; 7\}$

+) $a, b, c \equiv 2 (\mod 3) \Rightarrow a, b, c \in \{2; 5; 8\}$ .

+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2.

Giải chi tiết:

Bước 1:

Gọi số cần tìm là $\bar{a b c}$

Từ các số bài cho ta chia thành 3 bộ số:

+ Bộ số chia hết cho 3 là: 3; 6; 9

+ Bộ số chia cho 3 dư 1 là: 1; 4; 7

+ Bộ số chia cho 3 dư 2 là: 2; 5; 8

Bước 2:

Xét các trường hợp sau:

+) a, b, c đều chia hết cho 3 $\Rightarrow a, b, c = {3; 6; 9}$ Có 3! số.

+) $a, b, c \equiv 1 (\mod 3) \Rightarrow a, b, c \in \{1; 4; 7\}$ => Có 3! số.

+) $a, b, c \equiv 2 (\mod 3) \Rightarrow a, b, c \in \{2; 5; 8\}$ ⇒ Có 3!số.

+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2

$3! . C_{3}^{1} . C_{3}^{1} . C_{3}^{1} = 162$

Vậy có 3.3!+162=180 số thỏa mãn đề bài.

Câu 3

Một lô hàng có 30 sản phẩm trong đó có 5 phế phẩm. Lấy ngẫu nhiên đồng thời 6 sản phẩm của lô hàng đó. Xác suất để trong 6 sản phẩm lấy ra có không quá 2 phế phẩm là

A. $\frac{2530}{2639}$

B. $\frac{253}{263}$

C. $\frac{253}{280}$

D. $\frac{2535}{2737}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một ô tô đang chạy thì người lái đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc $v (t) = a - 80 t (m / s)$ trong đó t (giây) là khoảng thời gian tính từ lúc bắt đầu đạp phanh và a là một hằng số dương. Biết rằng từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được 36m. Khẳng định nào sau đây đúng?

A. aÎ(18,21)

B. aÎ(25,28)

C. aÎ(15,18)

D. aÎ(23,25)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình nón có bán kính đáy bẳng a. Thiết diện qua trục của hình nón là một tam giác đều. Thể tich khối nón đã cho bằng

A. $\frac{π a^{3} \sqrt{3}}{2}$

B. $π a^{3} \sqrt{3}$

C. $\frac{π a^{3} \sqrt{3}}{3}$

D. $\frac{π a^{3} \sqrt{2}}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một người vay ngân hàng với số tiền 50.000.000 đồng, mỗi tháng trả góp số tiền 4.000.000 đồng vào cuối tháng và phải trả lãi suất cho số tiền chưa trả là 1% một tháng theo hình thức lãi kép. Theo quy định, nếu người vay trả trước hạn thì sẽ chịu thêm phí phạt bằng 3% số tiền trả trước hạn. Hết tháng thứ 6, người đó muốn trả hết nợ. Tổng số tiền người đó phải trả cho ngân hàng là

A. 54.886.000 đồng.

B. 53.322.000 đồng.

C. 53.864.000 đồng.

D. 52.468.000 đồng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho hình chóp S ABC có SA ^ ( ABC ), tam giác ABC vuông tại B , SA = BC = a , AC = 2 a. Khoảng cách từ điểm A đến mặt phẳng (SBC) là

Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau và số đó chia hết cho 3.

Một lô hàng có 30 sản phẩm trong đó có 5 phế phẩm. Lấy ngẫu nhiên đồng thời 6 sản phẩm của lô hàng đó. Xác suất để trong 6 sản phẩm lấy ra có không quá 2 phế phẩm là

Cho hình nón có bán kính đáy bẳng a. Thiết diện qua trục của hình nón là một tam giác đều. Thể tich khối nón đã cho bằng

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu