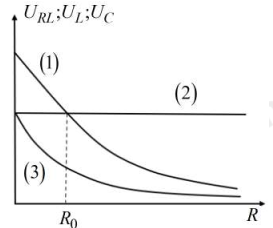
Cho mạch điện xoay chiều theo thứ tự tụ điện có điện dung C, điện trở R và cuộn dây thuần cảm có độ tử cảm L mắc nối tiếp. Đặt vào hai đầu mạch điện áp xoay chiều ổn định có dạng \[u = U\sqrt 2 \cos (\omega t)(V).\] Gọi \[{U_{RL}}\] là điện áp hiệu dụng ở hai đầu cuộn cảm L và biến trở R, U_C là điện áp hiệu dụng ở hai đầu cuộn cảm L. Đồ thị biểu diễn sự phụ thuộc của \[{U_{RL}},{U_C},{U_L}\] theo giá trị của R như trên hình vẽ. Khi R = 3R₀ thì độ lệch pha giữa hiệu điện thế hai đầu mạch và cường độ dòng điện là φ (rad). Giá trị φ gần nhất với giá trị nào sau đây?

Phương pháp: 

Sử dụng biểu thức tính dung kháng: \[{Z_C} = \frac{1}{{\omega C}}\]

Cách giải: 

Dung kháng của tụ điện: \[{Z_C} = \frac{1}{{\omega C}}\]

Phương pháp: 

+ Vận dụng biểu thức tính cảm kháng và dung kháng: \[\left\{ {\begin{array}{*{20}{l}}{{Z_L} = \omega L}\\{{Z_C} = \frac{1}{{\omega C}}}\end{array}} \right.\]

+ Sử dụng biểu thức tính hệ số công suất: $\cos \phi \mathrm{ }=\frac{R}{Z}$

Cách giải: 

+ Khi \[f = {f_2} = 50Hz:\cos {\varphi _2} = 1 \Rightarrow {Z_{{L_2}}} = {Z_{{C_2}}} \Leftrightarrow \frac{1}{{LC}} = \omega _2^2\]

+ Khi \[f = {f_1} = 25Hz:\left\{ {\begin{array}{*{20}{l}}{{Z_{{L_1}}} = \frac{{{\omega _1}}}{{{\omega _2}}}{Z_{{L_2}}} = \frac{{{Z_{{L_2}}}}}{2}}\\{{Z_{{C_1}}} = \frac{{{\omega _2}}}{{{\omega _1}}}{Z_{{C_2}}} = 2{Z_{{C_2}}} = 2{Z_{{L_2}}}}\end{array}} \right.\]

\[ \Rightarrow \cos {\varphi _1} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)}^2}} }} = \frac{R}{{\sqrt {{R^2} + \left( {\frac{{{Z_{{L_2}}}}}{2} - 2{Z_{{L_2}}}} \right)} }} = \frac{{\sqrt 2 }}{2}\] \[ \Rightarrow 2{R^2} = {R^2} + \frac{9}{4}Z_{{L_2}}^2 \Rightarrow {Z_{{L_2}}} = \frac{2}{3}R\]  

+ Khi \[f = {f_3} = 75Hz:\left\{ {\begin{array}{*{20}{l}}{{Z_{{L_3}}} = \frac{{{\omega _3}}}{{{\omega _2}}}{Z_{{L_2}}} = \frac{{3{Z_{{L_2}}}}}{2}}\\{{Z_{{C_3}}} = \frac{{{\omega _2}}}{{{\omega _3}}}{Z_{{C_2}}} = \frac{2}{3}{Z_{{C_2}}} = \frac{2}{3}{Z_{{L_2}}}}\end{array}} \right.\]

\[ \Rightarrow \cos {\varphi _3} = \frac{R}{{\sqrt {{R^2} + {{\left( {{Z_{{L_3}}} - {Z_{{C_3}}}} \right)}^2}} }} = \frac{R}{{\sqrt {{R^2} + \left( {\frac{{3{Z_{{L_2}}}}}{2} - \frac{2}{3}{Z_{{L_2}}}} \right)} }} = 0,874\]  Chọn B.