Trong môi trường đẳng hướng và không hấp thụ âm, trên mặt phẳng nằm ngang có 3 điểm O, M, N tạo thành tam giác vuông tại O, với \(OM = 80\;{\rm{m}},ON = 60\;{\rm{m}}.\) Đặt tại O một nguồn điểm phát âm có công suất P không đổi thì mức cường độ âm tại M là 50 dB. Mức cường độ âm lớn nhất trên đoạn MN gần nhất với giá trị nào sau đây?
A. 54,4dB.
Quảng cáo
Trả lời:
Phương pháp:
Công thức xác định mức cường độ âm: \(L = 10\log \frac{I}{{{I_0}}}\)
Công thức tính cường độ âm: \(I = \frac{P}{{4\pi {r^2}}}\)
Áp dụng hệ thức lượng trong tam giác vuông.
Cách giải:
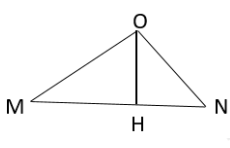
Công thức tính mức cường độ âm trên đoạn MN:
Với r là khoảng cách từ O đến 1 điểm trên MN.
⇒ \({L_{\max }} \Leftrightarrow {r_{\min }} = OH\) (với H là chân đường cao kẻ từ O xuống MN).
Áp dụng hệ thức lượng trong tam giác vuông OMN có:
\(OH = \frac{{OM \cdot ON}}{{MN}} = \frac{{80.60}}{{100}} = 48(\;{\rm{mm}})\)
Lại có:
\( \Rightarrow {L_H} = 50 + 20\log \frac{{OM}}{{OH}} = 50 + 20\log \frac{{80}}{{48}} \approx 54,4dB\)
Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Phương pháp:
Công thức liên hệ giữa tần số và bước sóng: \(f = \frac{c}{\lambda } \Rightarrow f - \frac{1}{\lambda }\)
Bước sóng theo thứ tự tăng dần: Tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại
Cách giải:
Bảng thang sóng điện từ:
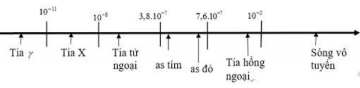
Có \(f = \frac{c}{\lambda } \Rightarrow f - \frac{1}{\lambda }\)
Tần số các sóng điện từ theo thứ tự giảm dần là: Tia tử ngoại, ánh sáng nhìn thấy, tia hồng ngoại.
Chọn A.
Câu 2
Lời giải
Phương pháp:
+ Bước sóng:
+ Điều kiện có cực đại giao thoa: \({d_2} - {d_1} = k\lambda ;k \in Z\)
Cách giải:
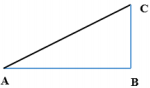
Phương trình dao động của hai nguồn:
\({u_A} = {u_B} = 5\cos \left( {20\pi t + \frac{{3\pi }}{4}} \right)({\rm{cm}};s)\)
Tốc độ truyền sóng: \(v = 0,2\;{\rm{m}}/{\rm{s}}\)
Bước sóng:
Bài cho \(AB = 30\;{\rm{cm}} \Rightarrow {\rm{AB}} = 15\lambda \)
Áp dụng định lí Pitago trong tam giác vuông ABC ta có: \(A{C^2} = A{B^2} + B{C^2} \Rightarrow A{B^2} = A{C^2} - B{C^2}\)
Mà:
Mặt khác: \({d_2} - {d_1} = k\lambda \left( 2 \right)\) (cực đại)
Từ (1) và (2) \( \Rightarrow {d_2} + {d_1} = \frac{{225}}{k}\lambda \)
Để cực đại cùng pha thì k và \(\frac{{225}}{k}\) hoặc cùng chẵn hoặc cùng lẻ, ở đây chỉ có k lẻ thỏa mãn.
Lại có: \({d_2} + {d_1} > 15\lambda \) (tổng hai cạnh bất kì của một tam giác luôn lớn hơn cạnh còn lại)
Lập bảng tìm các giá trị của k thỏa mãn:
|
k |
1 |
3 |
5 |
9 |
|
225 |
75 |
45 |
25 |
Để gần B nhất thì \({\left( {{d_2} + {d_1}} \right)_{\min }} \Leftrightarrow {\left( {\frac{{225}}{k}\lambda } \right)_{\min }} \Leftrightarrow {k_{\max }} = 9\)
Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.