Câu hỏi:

18/05/2022 457

Một máy đang phát sóng điện từ ở Hà Nội có phương truyền thẳng đứng hướng lên. Vào một thời điểm, tại điểm M trên phương truyền, véc-tơ cường độ điện trường đang có độ lớn bằng một nửa giá trị cực đại và hướng về phía Nam. Khi đó véc-tơ cảm ứng từ có

A. độ lớn cực đại và hướng về phía Bắc.

B. độ lớn bằng không.

C. độ lớn bằng một nửa giá trị cực đại và hướng về phía Đông.

D. độ lớn bằng một nửa giá trị cực đại và hướng về phía Tây.

Xem lời giải

Câu hỏi trong đề: 30 đề thi thử THPT Quốc gia môn Vật lí năm 2022 có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp:

Các vecto $\vec E,\vec B$ và hướng truyền sóng đôi một vuông góc với nhau tuân theo quy tắc bàn tay phải: đặt bàn tay phải sao cho vecto $\overrightarrow B $ hướng vào lòng bàn tay, ngón tay cái choãi ra chỉ chiều của $\overrightarrow E $ , bốn ngón tay hướng theo chiều truyền sóng điện từ

Trong sóng điện từ, điện trường và từ trường luôn biến thiên cùng pha: $\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}}$

Cách giải:

Nhận xét: điện trường và từ trường biến thiên cùng pha, ta có:

$\frac{E}{{{E_0}}} = \frac{B}{{{B_0}}} = \frac{1}{2} \Rightarrow B = \frac{{{B_0}}}{2}$

Áp dụng quy tắc bàn tay phải, ta có hình vẽ:

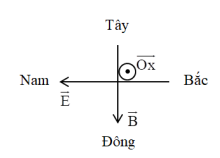
Một máy đang phát sóng điện từ ở Hà Nội có phương truyền thẳng đứng hướng lên. Vào một thời điểm, tại điểm M trên phương (ảnh 1)

Từ hình vẽ ta thấy vecto cảm ứng từ hướng về phía Đông

Chọn C.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chọn phát biểu đúng khi nói về đường sức điện.

A. Qua mỗi điểm trong điện trường ta có thể vẽ được ít nhất hai đường sức điện.

B. Các đường sức điện không cắt nhau.

C. Nơi nào điện trường mạnh hơn thì nơi đó đường sức điện được vẽ thưa hơn.

D. Các đường sức điện xuất phát từ các điện tích âm.

Lời giải

Phương pháp:

Sử dụng lý thuyết đường sức điện

Cách giải:

Qua mỗi điểm trong điện trường ta chỉ có thể vẽ được một đường sức điện → A sai

Các đường sức điện không bao giờ cắt nhau → B đúng

Nơi nào điện trường mạnh hơn thì nơi đó đường sức điện được vẽ mau hơn → C sai

Các đường sức điện xuất phát từ các điện tích dương và tận cùng ở các điện tích âm → D sai

Chọn B.

Câu 2

Một mạch dao động LC, với cuộn cảm thuần L = 9 mH. Trong quá trình dao động, hiệu điện thế cực đại giữa hai bản tụ là 12 V. Tại thời điểm điện tích trên bản tụ có độ lớn q = 24 nC thì dòng điện trong mạch có cường độ $i = 4\sqrt 3 mA$. Chu kì dao động riêng của mạch bằng

A. 12π μs.

B. 6π μs.

C. 6π ms.

D. 12π ms.

Lời giải

Phương pháp:

Định luật bảo toàn năng lượng điện từ: ${{\rm{W}}_d} = {{\rm{W}}_t} \Rightarrow \frac{1}{2}CU_0^2 = \frac{1}{2}LI_0^2$

Công thức độc lập với thời gian: $\frac{{{q^2}}}{{q_0^2}} + \frac{{{i^2}}}{{I_0^2}} = 1$

Chu kì dao động riêng của mạch: $T = 2\pi \sqrt {LC} $

Cách giải:

Áp dụng định luật bảo toàn năng lượng điện từ trong mạch, ta có:

${{\rm{W}}_{d{\rm{max}}}} = {{\rm{W}}_{t\max }} \Rightarrow \frac{1}{2}{\rm{CU}}_0^2 = \frac{1}{2}LI_0^2 \Rightarrow I_0^2 = \frac{{CU_0^2}}{L} = \frac{{C{{.12}^2}}}{{{{9.10}^{ - 3}}}} = 16000{\rm{C}}$

Áp dụng công thức độc lập với thời gian, ta có:

$\frac{q^{2}}{q_{0}^{2}} + \frac{i^{2}}{I_{0}^{2}} = 1 \Rightarrow \frac{q^{2}}{C^{2} U_{0}^{2}} + \frac{i^{2}}{I_{0}^{2}} = 1 \Rightarrow \frac{{({24.10}^{- 9})}^{2}}{C^{2} {.12}^{2}} + \frac{{(4 \sqrt{3} \cdot 10^{- 3})}^{2}}{16000 C} = 1$

$\Rightarrow [\begin{matrix} \frac{1}{C} = {25.10}^{7} \Rightarrow C = {4.10}^{- 9} (F) {\frac{1}{C} = - {1.10}^{9} (loai) \end{matrix}$
Chu kì dao động riêng của mạch là: