Câu hỏi:
18/05/2022 634
Trên mặt chất lỏng có hai nguồn sóng cùng tần số, cùng pha đặt tại hai điểm A và B. Cho bước sóng do các nguồn gây ra là λ = 5cm. Trên nửa đường thẳng đi qua B trên mặt chất lỏng có hai điểm M và N (N gần B hơn). Điểm M dao động với biên độ cực đại, N dao động với biên độ cực tiểu, giữa M và N có ba điểm dao động với biên độ cực đại khác. Biết hiệu MA – NA = 3,2 cm. Nếu đặt hai nguồn sóng này tại M và N thì số điểm dao động với biên độ cực đại trên đoạn thẳng AB là
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
Điều kiện tại một điểm là cực đại giao thoa: \(MA - MB = k\lambda \)
Điều kiện tại một điểm là cực tiểu giao thoa: \(NA - NB = (k + 0,5)\lambda \)
Số điểm dao động với biên độ cực đại trên đoạn thẳn AB thỏa mãn:
Cách giải: Ta có hình vẽ:
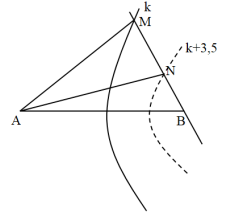
Giả sử tại M là cực đại bậc k
Giữa M, N có 3 cực đại nữa → tại N là cực tiểu thức k + 3,5
Ta có:
Đặt hai nguồn sóng tại MN, điểm B nằm trên đường thẳng MN, số điểm dao động với biên độ cực đại trên đoạn AB thỏa mãn:
→ Trên AB có 4 điểm dao động với biên độ cực đại
Chọn D.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Một mạch dao động LC, với cuộn cảm thuần L = 9 mH. Trong quá trình dao động, hiệu điện thế cực đại giữa hai bản tụ là 12 V. Tại thời điểm điện tích trên bản tụ có độ lớn q = 24 nC thì dòng điện trong mạch có cường độ \(i = 4\sqrt 3 mA\). Chu kì dao động riêng của mạch bằng
Xem đáp án »
18/05/2022
1,614
Câu 3:
Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc, khoảng cách giữa hai khe là 1 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn là 2 m. Trong hệ vân trên màn, vân sáng bậc 3 cách vân trung tâm 2,4 mm. Bước sóng của ánh sáng đơn sắc dùng trong thí nghiệm là
Xem đáp án »
18/05/2022
1,374
Câu 4:
Dùng một ampe kế nhiệt để đo cường độ dòng điện trong một mạch điện xoay chiều, số chỉ của ampe kế cho biết
Xem đáp án »
18/05/2022
1,234
Câu 5:
Hạt α có động năng 5 MeV bắn vào một hạt nhân \(_4^9Be\) đứng yên, gây ra phản ứng tạo thành một hạt \(^{12}C\) và một hạt nơtron. Hai hạt sinh ra có vectơ vận tốc hợp với nhau một góc 800. Cho biết phản ứng tỏa ra năng lượng 5,6 MeV. Coi khối lượng xấp xỉ bằng số khối. Động năng của hạt nhân 12C có thể bằng
Xem đáp án »
18/05/2022
876
Câu 6:
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình li độ lần lượt là \({x_1} = {A_1}\cos \left( {10t + \frac{\pi }{6}} \right)(cm);{x_2} = 4\cos (10t + \varphi )(cm)\) (t tính bằng s), \({A_1}\) có giá trị thay đổi được. Phương trình dao động tổng hợp của vật có dạng \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)(cm)\). Độ lớn gia tốc lớn nhất của vật có thể nhận giá trị là
Xem đáp án »
18/05/2022
734
Câu 7:
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch AB mắc nối tiếp theo thứ tự gồm cuộn cảm thuần L, biến trở R và tụ điện C. Gọi ULR là điện áp hiệu dụng ở hai đầu đoạn mạch gồm cuộn cảm thuần L và biến trở R, UC là điện áp hiệu dụng ở hai đầu tụ C, UL là điện áp hiệu dụng hai đầu cuộn cảm thuần L. Hình bên là đồ thị biểu diễn sự phụ thuộc của, \[{U_{LR}},{U_L},{U_C}\] theo giá trị của biến trở R. Khi \[R = 1,5{R_0}\] thì hệ số công suất của đoạn mạch AB xấp xỉ là
Xem đáp án »
18/05/2022
698
🔥 Đề thi HOT:
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Bình Phước có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí Cụm các trường THPT , Các trung tâm GDTX , GDNN - GDTX Tỉnh Bắc Ninh có đáp án
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 26)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận