Câu hỏi:

21/05/2022 2,558

Cho hình lăng trụ đều ABC.A’B’C’ có độ dài tất cả các cạnh bằng a. Gọi M là trung điểm AB và N là điểm thuộc cạnh AC sao cho CN = 2AN. Thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’ bằng:

A. $\frac{5 \sqrt{3} a^{3}}{12} .$

B. $\frac{\sqrt{3} a^{3}}{36} .$

C. $\frac{5 \sqrt{3} a^{3}}{36} .$

D. $\frac{\sqrt{3} a^{3}}{12} .$

Xem lời giải

Câu hỏi trong đề: Top 5 đề thi Đánh giá năng lực trường ĐH Bách khoa Hà Nội năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Cách 1.

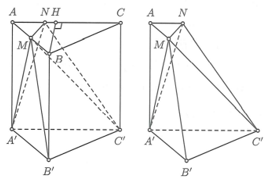
Cho hình lăng trụ đều ABC.A’B’C’ có độ dài tất cả các cạnh bằng a. (ảnh 1)

Gọi V là thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’.

Khi đó ta có $V = V_{M . A' A N} + V_{M . A' C' N} + V_{M . A' B' C'}$

Từ giả thiết ta có

$S_{Δ A' A N} = \frac{1}{2} A A' . A N = \frac{1}{2} . a . \frac{a}{3} = \frac{a^{2}}{6}; S_{Δ A' C' N} = \frac{1}{2} d (N, A' C') . A' C' = \frac{1}{2} . a . a = \frac{a^{2}}{2};$

$S_{Δ A' B' C'} = \frac{1}{2} A' B' . A' C' . s i n 60^{o} = \frac{a^{2} \sqrt{3}}{4}$

Gọi H là trung điểm của $A C \Rightarrow B H ⊥ (A C C' A')$ và $B H = \frac{a \sqrt{3}}{2}$

$\Rightarrow d (M, (A C C' A')) = \frac{1}{2} d (B, (A C C' A')) = \frac{1}{2} B H = \frac{a \sqrt{3}}{4} .$

Khi đó ta có

$V_{M . A' A N} = \frac{1}{3} d (M; (A C C' A')) . S_{Δ A' A N} = \frac{1}{3} . \frac{a \sqrt{3}}{4} . \frac{a^{2}}{6} = \frac{a^{3} \sqrt{3}}{72} .$

$\begin{array}{l} V_{M . A' C' N} = \frac{1}{3} d (M, (A C C' A')) . S_{Δ A' C' N} = \frac{1}{3} . \frac{a \sqrt{3}}{4} . \frac{a^{2}}{2} = \frac{a^{3} \sqrt{3}}{24} . \\ V_{M . A' B' C'} = \frac{1}{3} d (M, (A' B' C')) . S_{Δ A' B' C'} = \frac{1}{3} . a . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{3} \sqrt{3}}{12} . \end{array}$ Vậy $V = V_{M . A' A N} + V_{M . A' C' N} + V_{M . A' B' C'} = \frac{a^{3} \sqrt{3}}{72} + \frac{a^{3} \sqrt{3}}{24} + \frac{a^{3} \sqrt{3}}{12} = \frac{5 \sqrt{3} a^{3}}{36}$

Cách 2.

Gọi V là thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’. Khi đó ta có

$V = V_{M . A A' C' N} + V_{M . A' B' C'}$ .

Ta có $S_{A A' C' N} = \frac{1}{2} A A' (A N + A' C') = \frac{1}{2} a (\frac{a}{3} + a) = \frac{2 a^{2}}{3} .$

Suy ra $V_{M . A A' C' N} = \frac{1}{3} d (M, (A C C' A')) . S_{A A' C' N} = \frac{1}{3} . \frac{a \sqrt{3}}{4} . \frac{2 a^{3}}{3} = \frac{2 \sqrt{3} a^{3}}{36}$

$V_{M . A' B' C'} = \frac{1}{3} d (M, (A' B' C')) . S_{Δ A' B' C'} = \frac{1}{3} . a . \frac{a^{2} \sqrt{3}}{4} = \frac{a^{3} \sqrt{3}}{12} .$

Vậy $V = V_{M . A A' C' N} + V_{M . A' B' C'} = \frac{2 \sqrt{3} a^{3}}{36} + \frac{a^{3} \sqrt{3}}{12} = \frac{5 \sqrt{3} a^{3}}{36} .$

Cách 3.

Gọi H là trung điểm của AC và V là thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’.

Khi đó, $V = V_{A M H . A' B' C'} - V_{M . N H C'}$

Dễ thấy $M H / / B' C'$ nên AMH.A’B’C’ là khối chóp cụt.

Áp dụng công thức thể tích V₁ của khối chóp cụt có chiều cao h, diện tích đáy nhỏ và đáy lớn theo thứ tự là S₀, S₁ thì ta có

$V_{1} = \frac{h}{3} (S_{0} + \sqrt{S_{0} S_{1}} + S_{1})$

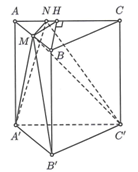
Khi đó

$V_{A M H . A' B' C'} = \frac{A A'}{3} (S_{A M H} + \sqrt{S_{A M H} . S_{A' B' C'}} + S_{A' B' C'})$

$= \frac{a}{3} (\frac{1}{4} . \frac{a^{2} \sqrt{3}}{4} + \sqrt{\frac{1}{4} . \frac{a^{2} \sqrt{3}}{4} . \frac{a^{2} \sqrt{3}}{4}} + \frac{a^{2} \sqrt{3}}{4}) = \frac{7 a^{3} \sqrt{3}}{48}$

Mặt khác, $V_{M . N H C'} = \frac{1}{3} d (M, (A C C' A')) . S_{N H C'} = \frac{1}{3} . \frac{a \sqrt{3}}{4} . \frac{1}{2} . a . \frac{a}{6} = \frac{a^{3} \sqrt{3}}{144}$

Vậy $V = V_{A M H . A' B' C'} - V_{M . N H C' .} = \frac{7 a^{3} \sqrt{3}}{48} - \frac{a^{3} \sqrt{3}}{144} = \frac{5 \sqrt{3} a^{3}}{36}$

Chọn C

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một thùng rượu có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách đều hai đáy có bán kính là 40cm, chiều cao thùng rượu là 1m. Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu là bao nhiêu?

A. 425162 lít.

B. 212581 lít.

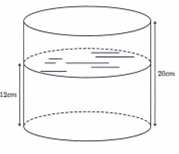
C. 212,6 lít.

D. 425,2 lít.

Lời giải

Đặt mặt cắt qua trục của thùng rượu lên hệ trục tọa độ

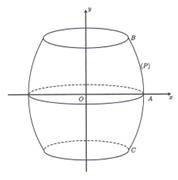
Một thùng rượu có bán kính các đáy là 30cm, (ảnh 2)

Oxy như hình vẽ. Đơn vị tính là dm.

Gọi $(P) : x = a y^{2} + b y + c$ qua $A (4; 0), B (3; 5), C (3; - 5)$

Thể tích của thùng rượu là $\Rightarrow \{\begin{cases} a = - \frac{1}{25} \\ b = 0 \\ c = 4 \end{cases} \Rightarrow (P) : x = - \frac{1}{25} y^{2} + 4$

$V = π \int_{- 5}^{5} {(- \frac{1}{25} y^{2} + 4)}^{2} d y ≃ 425, 2 (d m^{3}) = 425, 2 (l)$

Chọn D

Câu 2

Một cốc hình trụ có bán kính đáy bằng 3cm, chiều cao 20cm, trong cốc đang có một ít nước, khoảng cách giữa đáy cốc và mặt nước là 12cm. Một con quạ muốn uống nước được trong cốc thì mặt nước phải cách miệng cốc không quá 6cm. Con quạ thông minh đã mổ những viên sỏi hình cầu có bán kính 0,8cm thả vào cốc để mực nước dâng lên. Hỏi để uống được nước, con quạ cần thả ít nhất bao nhiêu viên sỏi?

A. 26

B. 27

C. 28

D. 29

Lời giải

Con quạ uống được nước đựng trong cốc khi có mặt nước cách miệng cốc không quá 6cm nên mực nước dâng lên tối thiểu là 20 – 12 – 6 = 2 cm.

Thể tích nước tối thiểu cần tăng thêm là $V = π R^{2} h = π {.3}^{2} .2 = 18 π (c m^{3})$

Thể tích nước tăng lên khi con quạ thả x viên sỏi là:

$V_{1} = x . \frac{4}{3} π r^{3} = x . \frac{4}{3} . π .0, 8^{3} = \frac{256}{375} π x (c m^{3})$

Để con quạ uống được nước ta có điều kiện $V_{1} \geq V \Leftrightarrow \frac{256}{375} π x \geq 18 π \Leftrightarrow x \geq 26, 37$

Vậy con quạ cần thả ít nhất 27 viên sỏi để uống được nước trong cốc.

Chọn B

Câu 3

Hai nhà khoa học Andre Geim và Konstantin Novoselov được trao giải Nobel có công trình phân lập graphene vào năm nào?

A. 2004

B. 2006

C. 2008

D. 2010

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một người thợ được yêu cầu trang trí trên một bức tường hình vuông kích thước 5m x 5m bằng cách vẽ một hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu, tô kín màu lên hai tam giác đối diện bằng cách sử dụng hai màu xanh (phần chấm) và hồng (phần tô màu). Quá trình vẽ và tô theo quy luật đó được lặp lại 6 lần. Tính số tiền mua sơn để người thợ đó hoàn thành công việc trang trí theo yêu cầu trên gần nhất với con số nào trong bốn đáp án dưới đây, biết tiền sơn màu xanh để sơn kín 1m² là 100000 đồng và tiền sơn màu hồng đắt gấp 1,5 so với tiền sơn màu xanh.

A. 1540000 đồng.

B. 1570000 đồng.

C. 1650000 đồng.

D. 1480000 đồng.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tứ diện ABCD có $\hat{A B C} = \hat{A D C} = \hat{B C D} = 90^{o}$ , $B C = 2 a, C D = a,$ góc giữa đường thẳng AB và mặt phẳng (BCD) bằng $60^{o}$ . Tính khoảng cách giữa hai đường thẳng AC và BD

A. $\frac{a \sqrt{6}}{\sqrt{31} .}$

B. $\frac{2 a \sqrt{6}}{\sqrt{31} .}$

C. $\frac{2 a \sqrt{3}}{\sqrt{31}} .$

D. $\frac{a \sqrt{3}}{\sqrt{31} .}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số $y = \frac{(4 - m) \sqrt{6 - x} + 3}{\sqrt{6 - x} + m}$ . Có bao nhiêu giá trị nguyên của m trong khoảng (-10;10) sao cho hàm số đồng biến trên khoảng (-8;5)?

A. 14

B. 13

C. 12

D. 15

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình lăng trụ đều ABC.A’B’C’ có độ dài tất cả các cạnh bằng a. Gọi M là trung điểm AB và N là điểm thuộc cạnh AC sao cho CN = 2AN. Thể tích của khối đa diện lồi có các đỉnh là các điểm A, M, N, A’, B’ và C’ bằng:

Bình luận

Hai nhà khoa học Andre Geim và Konstantin Novoselov được trao giải Nobel có công trình phân lập graphene vào năm nào?

Cho tứ diện ABCD có ABC^=ADC^=BCD^=90o ,BC=2a,CD=a, góc giữa đường thẳng AB và mặt phẳng (BCD) bằng 60o . Tính khoảng cách giữa hai đường thẳng AC và BD

Cho hàm số y=4−m6−x+36−x+m . Có bao nhiêu giá trị nguyên của m trong khoảng (-10;10) sao cho hàm số đồng biến trên khoảng (-8;5)?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tứ diện ABCD có $\hat{A B C} = \hat{A D C} = \hat{B C D} = 90^{o}$ , $B C = 2 a, C D = a,$ góc giữa đường thẳng AB và mặt phẳng (BCD) bằng $60^{o}$ . Tính khoảng cách giữa hai đường thẳng AC và BD

Cho hàm số $y = \frac{(4 - m) \sqrt{6 - x} + 3}{\sqrt{6 - x} + m}$ . Có bao nhiêu giá trị nguyên của m trong khoảng (-10;10) sao cho hàm số đồng biến trên khoảng (-8;5)?