Câu hỏi:

13/07/2024 31,696

Một học sinh dự định vẽ các tấm thiệp xuân bằng tay để bàn trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mỗi loại để có được nhiều tiền nhất.

Xem lời giải

Câu hỏi trong đề: Bài tập Hệ bất phương trình bậc nhất hai ẩn có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi x (tấm), y (tấm) lần lượt là số thiệp loại nhỏ và số thiệp loại lớn mà bạn học sinh đó vẽ.

Hiển nhiên x ≥ 0 và y ≥ 0.

Học sinh này phải vẽ ít nhất 12 tấm nên ta có bất phương trình x + y ≥ 12.

Số giờ cần để làm x tấm thiệp nhỏ là : 2x (giờ).

Số giờ cần để làm y tấm thiệp lớn là : 3y (giờ).

Tổng số giờ để vẽ x tấm thiệp nhỏ và y tấm thiệp lớn là : 2x + 3y (giờ).

Vì học sinh này chỉ có 30 giờ để vẽ nên ta có bất phương trình : 2x + 3y ≤ 30.

Vậy ta có hệ bất phương trình:

$\{\begin{cases} x \geq 0 \\ y \geq 0 \\ x + y \geq 12 \\ 2 x + 3 y \leq 30 \end{cases}$

Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ Oxy ta được hình sau :

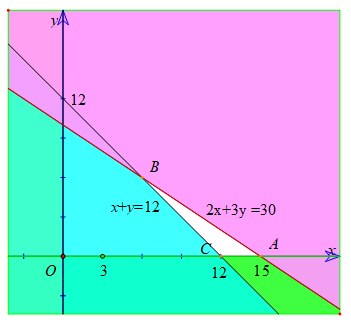
Media VietJack

Vậy, miền không tô màu (miền tam giác ABC, bao gồm cả các cạnh) trong hình sau là phần giao các miền nghiệm của các bất phương trình trong hệ và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình trên.

Tọa độ các đỉnh của tam giác đó là : A (15; 0); B(6; 6); C(12; 0).

Gọi F là số tiền (đơn vị: nghìn đồng) của việc bán x tấm thiệp nhỏ và y tấm thiệp lớn.

Số tiền thu được từ x tấm thiệp nhỏ là : 10x (nghìn đồng).

Số tiền thu được từ y tấm thiệp lớn là : 20y (nghìn đồng).

Tổng số tiền thu được là : 10x + 20y (nghìn đồng).

Vậy F =10x + 20y (nghìn đồng).

Ta phải tìm x, y thỏa mãn hệ bất phương trình sao cho F đạt giá trị lớn nhất, nghĩa là tìm giá trị lớn nhất của biểu thức F =10x + 20y trên miền tam giác ABC.

Tính các giá trị của F tại các đỉnh của tam giác, ta có :

Tại A(15 ; 0): F = 10.15 + 20.0 = 150 ;

Tại B(6 ; 6): F = 10.6 + 20.6 = 180 ;

Tại C(12 ; 0): F = 10.12 + 20.0 = 120 ;

F đạt giá trị lớn nhất bằng 180 tại B(6 ; 6).

Vậy để có được nhiều tiền nhất bạn ấy cần vẽ 6 tấm thiệp nhỏ và 6 tấm thiệp lớn.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một người bán nước giải khát đang có 24 g bột cam, 9 l nước và 210 g đường để pha chế hai loại nước cam A và B. Để pha chế 1 l nước cam loại A cần 30 g đường, 1 l nước và 1 g bột cam; để pha chế 1 l nước cam loại B cần 10 g đường, 1 l nước và 4 g bột cam. Mỗi lít nước cam loại A bán được 60 nghìn đồng, mỗi lít nước cam loại B bán được 80 nghìn đồng. Người đó nên pha chế bao nhiêu lít nước cam mỗi loại để có doanh thu cao nhất ?

Xem đáp án

Lời giải

Gọi x là số lít nước cam loại A và y là số lít nước cam loại B có thể pha chế được.

- Hiển nhiên x ≥ 0 và y ≥ 0.

Để pha chế x lít nước cam loại A cần 30x gam đường, x lít nước và x gam bột cam.

Để pha chế y lít nước cam loại B cần 10y gam đường, y lít nước và 4y gam bột cam.

Tổng số đường cần dùng là: 30x + 10y (g); tổng số nước cần dùng là x + y (l) ; tổng số bột cam cần dùng là: x + 4y (gam).

- Do chỉ có 210 gam đường nên ta có bất phương trình: 30x + 10y ≤ 210, hay 3x + y ≤ 21.

- Do chỉ có 9 l nước nên ta có bất phương trình: x + y ≤ 9.

- Do chỉ có 24 gam bột cam nên ta có bất phương trình: x + 4y ≤ 24

Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc đối với x và y là: $\{\begin{matrix} x \geq 0 \\ y \geq 0 \\ 3 x + y \leq 21 \\ \begin{array}{l} x + y \leq 9 \\ x + 4 y \leq 24 \end{array} \end{matrix}$

Biểu diễn miền nghiệm của hệ bất phương trình này trên hệ trục tọa độ Oxy, ta được hình 4.

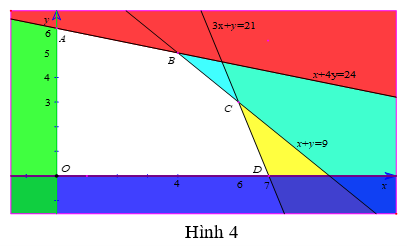
Media VietJack

Miền nghiệm của hệ bất phương trình là miền không tô màu (ngũ giác OABCD bao gồm cả các cạnh).

Tọa độ các đỉnh của ngũ giác đó là: O(0; 0); A (0; 6); B(4; 5); C(6; 3); D (7; 0).

Gọi F là doanh thu (đơn vị: nghìn đồng) của việc bán x lít nước cam loại A và y lít nước cam loại B.

Vì mỗi lít nước cam loại A bán được 60 nghìn đồng nên x lít nước cam loại A bán được 60x (nghìn đồng). Mỗi lít nước cam loại B bán được 80 nghìn đồng nên y lít nước cam loại B bán được 80y (nghìn đồng).

Tổng số tiền thu được là 60x + 80y (nghìn đồng)

Vì vậy, ta có: F(x ; y) = 60x + 80y.

Ta phải tìm x, y thỏa mãn hệ bất phương trình sao cho F đạt giá trị lớn nhất, nghĩa là tìm giá trị lớn nhất của biểu thức F = 60x + 80y trên miền ngũ giác OABCD.

Tính các giá trị của F tại các đỉnh của ngũ giác, ta có :

Tại O(0 ; 0) : F = 60.0 + 80.0 = 0 ;

Tại A(0 ; 6) : F = 60.0 + 80.6 = 480 ;

Tại B(4 ; 5) : F = 60.4 + 80.5 = 640 ;

Tại C(6 ; 3) : F = 60.6 + 80.3 = 600 ;

Tại D(7 ; 0) : F = 60.7 + 80.0 = 420 ;

F đạt giá trị lớn nhất bằng 640 tại B(4 ; 5).

Vậy để có doanh thu cao nhất thì người đó nên pha chế 4 lít nước cam loại A và 5 lít nước cam loại B.

Câu 2

Trong một tuần, bạn Mạnh có thể thu xếp được tối đa 12 giờ để tập thể dục giảm cân bằng hai môn : đạp xe và tập cử tạ tại phòng tập. Cho biết mỗi giờ đạp xe sẽ tiêu hao 350 calo và không tốn chi phí, mỗi giờ tập cử tạ sẽ tiêu hao 700 calo với chi phí 50 000 đồng/giờ. Mạnh muốn tiêu hao nhiều calo nhưng không được vượt quá 7 000 calo một tuần. Hãy giúp bạn Mạnh tính số giờ đạp xe và số giờ tập tạ một tuần trong hai trường hợp sau :

a) Mạnh muốn chi phí tập luyện là ít nhất.

b) Mạnh muốn số calo tiêu hao là lớn nhất.

Xem đáp án

Lời giải

Gọi x (giờ) là số giờ bạn Mạnh đạp xe, y (giờ) là số giờ bạn Mạnh tập tạ trong một tuần.

Hiển nhiên ta có x ≥ 0 và y ≥ 0.

Tổng số giờ bạn Mạnh tập thể dục trong một tuần là : x + y (giờ)

Do một tuần bạn Mạnh thu xếp được tối đa 12 giờ để tập thể dục nên ta có bất phương trình sau : x + y ≤ 12.

Do mỗi giờ đạp xe tiêu hao 350 calo nên với x giờ đạp xe sẽ tiêu hao 350x calo.

Mỗi giờ tập tạ tiêu hao 700 calo nên với y giờ tập tạ sẽ tiêu hao 700y calo.

Tổng số calo tiêu hao là : 350x + 700y (calo).

Mặt khác, Mạnh muốn tiêu hao nhiều calo nhưng không được vượt quá 7 000 calo một tuần. Vì vậy, ta có bất phương trình : 350x + 700y ≤ 7 000, tức là : x + 2y ≤ 20.

Vậy ta có hệ bất phương trình là :

$\{\begin{cases} x \geq 0 \\ y \geq 0 \\ x + y \leq 12 \\ x + 2 y \leq 20 \end{cases}$

Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ Oxy ta được hình ảnh sau :

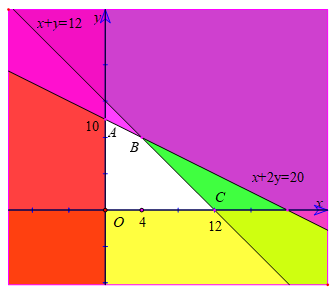
Media VietJack

Vậy, miền không tô màu (miền tứ giác OABC, bao gồm cả các cạnh) là phần giao miền nghiệm của các bất phương trình trong hệ và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình trên.

Tọa độ các đỉnh của tứ giác đó là : O(0 ;0) ; A (0; 10); B(4; 8); C(12; 0).

Gọi F là chi phí tập luyện.

Vì đạp xe không mất phí và tập tạ tốn chi phí 50 000 đồng/giờ nên với x giờ đạp xe và y giờ tập tạ thì tốn số tiền là : 0.x + 50 000y = 50 000y (đồng).

Vậy F =50 000y.

Tính các giá trị của F tại các đỉnh của tứ giác, ta có :

Tại O(0 ; 0) : F = 50 000.0 = 0;

Tại A(0 ; 10) : F = 50 000.10 = 500 000;

Tại B(4 ; 8) : F = 50 000. 8 = 400 000 ;

Tại C(12 ; 0) : F = 50 000 . 0 = 0 ;

F đạt giá trị nhỏ nhất bằng 0 tại O (0;0); C(12 ; 0).

Vậy Mạnh muốn chi phí tập luyện là ít nhất khi Mạnh không tập luyện cả hai môn thể thao trên hoặc Mạnh chỉ đạp xe 12 giờ và không tập tạ.

b) Gọi F’ là số calo tiêu hao. Khi đó F’ = 350x + 700y (calo).

Tính các giá trị của F’ tại các đỉnh của tứ giác, ta có :

Tại O(0 ; 0) : F’ = 350.0 + 700.0 = 0;

Tại A(0 ; 10) : F’ = 350.0 + 700.10 = 7 000;