Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ Oxy.
a) -2x + y - 1 ≤ 0;
b) -x + 2y > 0;
c) x – 5y < 2
d) -3x + y + 2 ≤ 0;
e) 3(x – 1) + 4(y – 2 ) < 5x – 3.
Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ Oxy.
a) -2x + y - 1 ≤ 0;
b) -x + 2y > 0;
c) x – 5y < 2
d) -3x + y + 2 ≤ 0;
e) 3(x – 1) + 4(y – 2 ) < 5x – 3.
Câu hỏi trong đề: Bài tập cuối chương II có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vẽ đường thẳng a: -2x + y - 1 = 0 đi qua hai điểm A(0; 1) và B(; 0).
Xét gốc tọa độ O(0 ;0). Ta thấy O ∉ a và -2.0 + 0 - 1 = -1 ≤ 0.
Suy ra (0 ; 0) là nghiệm của bất phương trình -2x + y - 1 ≤ 0.
Do đó, miền nghiệm của bất phương trình -2x + y - 1 ≤ 0 là nửa mặt phẳng kể cả bờ a, có chứa gốc O (là miền tô màu trong hình vẽ sau).
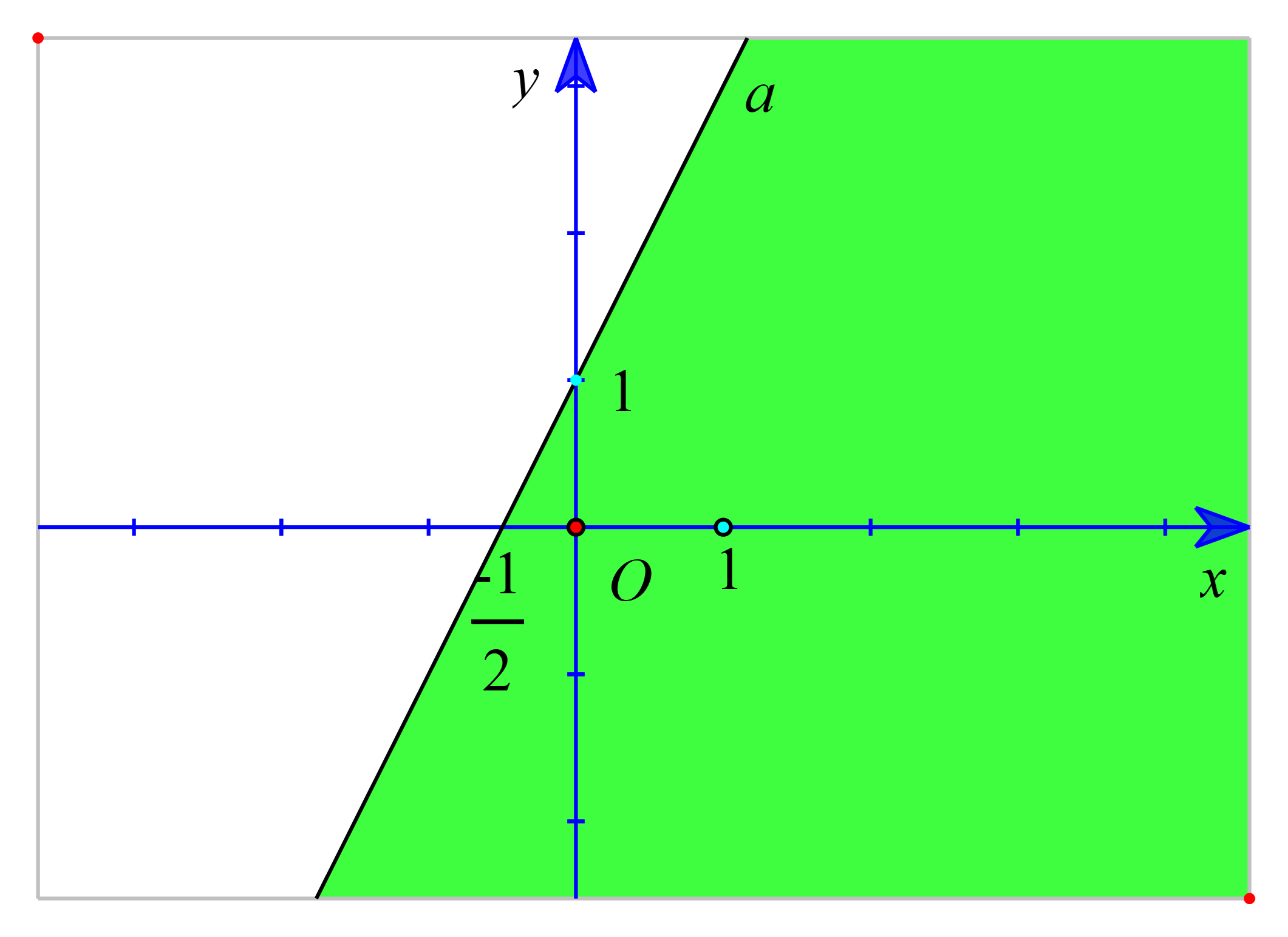
b) Vẽ đường thẳng b: - x + 2y = 0 đi qua hai điểm O(0; 0) và B(2 ;1).
Xét điểm C(0 ; 1). Ta thấy C ∉ b và - 0 + 2.1 = 2 > 0.
Suy ra (0 ; 1) là nghiệm của bất phương trình - x + 2y > 0
Do đó, miền nghiệm của bất phương trình - x + 2y > 0 là nửa mặt phẳng không kể bờ b, có chứa điểm C(0 ; 1) (là miền tô màu trong hình vẽ sau).
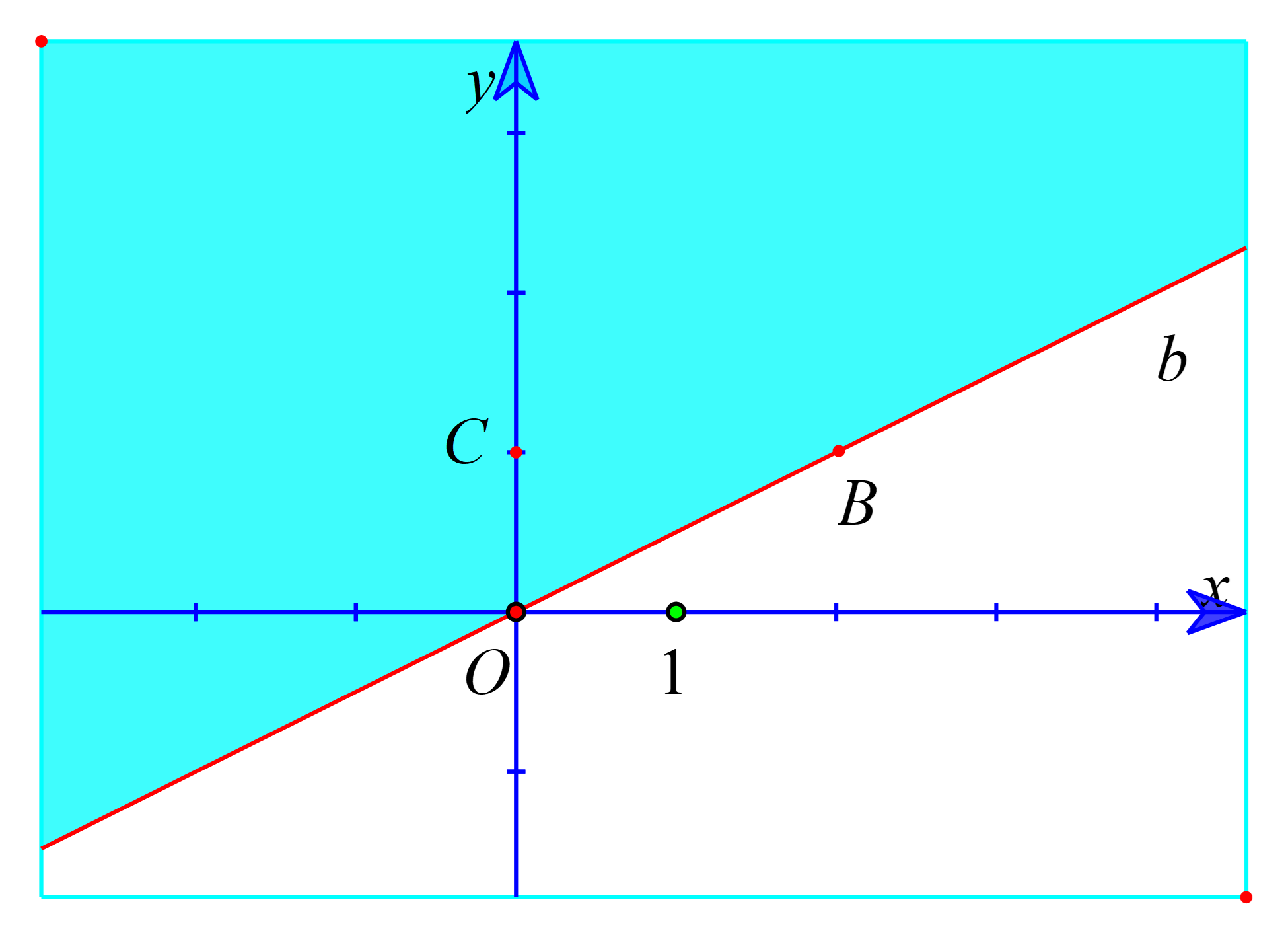
c) Ta có : x – 5y < 2 ⇔ x – 5y – 2 < 0
Vẽ đường thẳng c: x - 5y - 2 = 0 đi qua hai điểm A(0; ) và B(2 ; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ c và 0 – 5.0 – 2 = - 2 < 0.
Suy ra (0 ; 0) là nghiệm của bất phương trình x – 5y – 2 < 0
Do đó, miền nghiệm của bất phương trình x – 5y – 2 < 0 là nửa mặt phẳng không kể bờ c, có chứa gốc O (là miền tô màu trong hình vẽ sau).
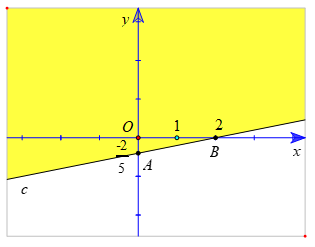
d) Vẽ đường thẳng d: -3x + y + 2 = 0 đi qua hai điểm A(0; -2) và B(; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ d và -3.0 + 0 + 2 = 2 > 0.
Suy ra (0 ; 0) không là nghiệm của bất phương trình -3x + y + 2 ≤ 0
Do đó, miền nghiệm của bất phương trình -3x + y + 2 ≤ 0 là nửa mặt phẳng kể cả bờ d, không chứa gốc O (là miền tô màu trong hình vẽ sau).
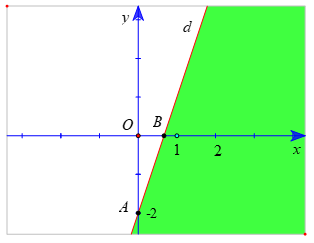
e) 3(x – 1) + 4(y – 2 ) < 5x – 3.
⇔ 3x – 3 + 4y – 8 < 5x – 3
⇔ 3x – 3 + 4y – 8 – 5x + 3 < 0
⇔ - 2x + 4y – 8 < 0
. ⇔ - x + 2y – 4 < 0.
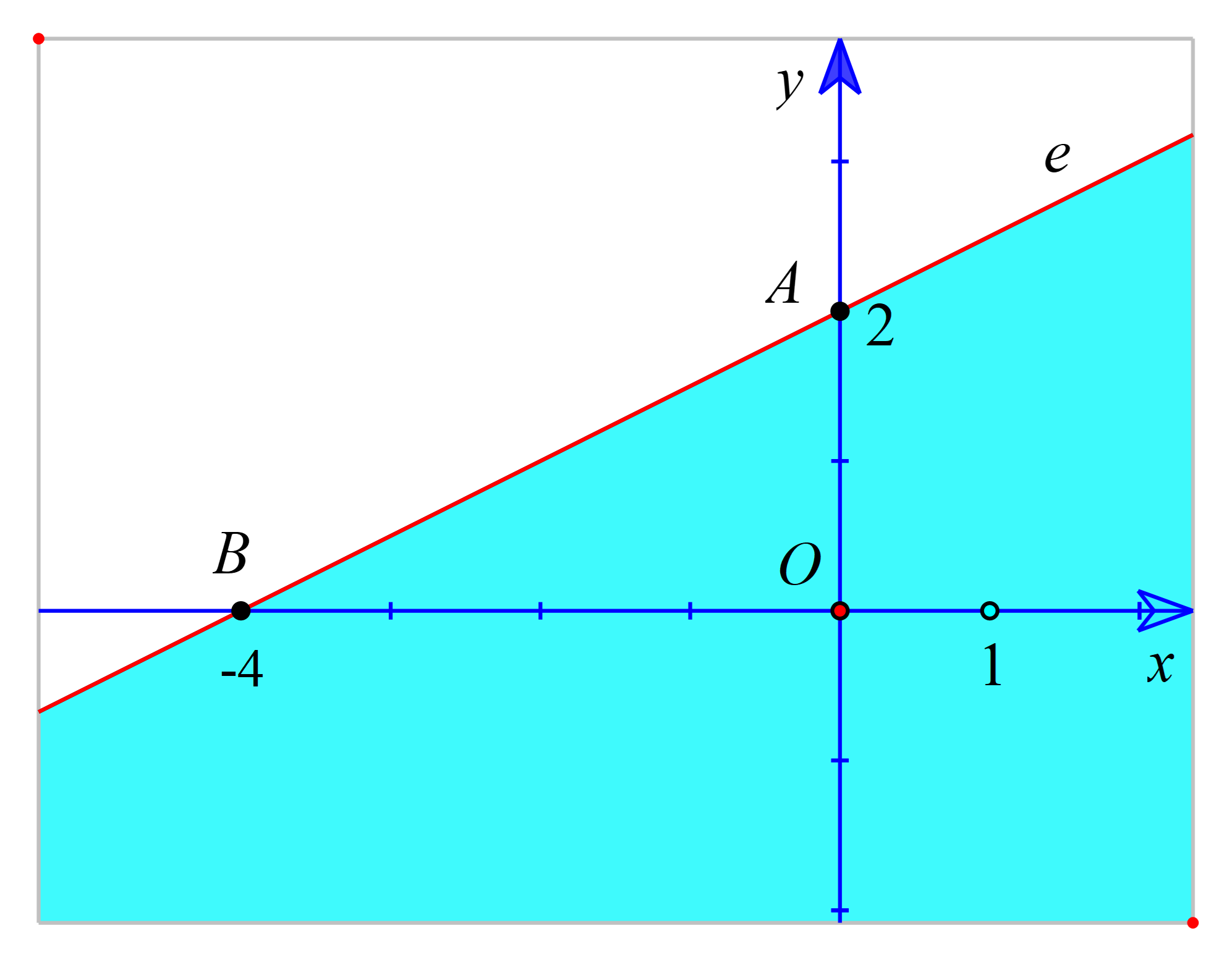
Vẽ đường thẳng e: - x + 2y – 4 = 0.đi qua hai điểm A(0; 2) và B(-4 ; 0).
Xét gốc tọa độ O(0 ;0). Ta thấy O ∉ e và - 0 + 2. 0 - 4 = - 4 < 0.
Suy ra (0 ; 0) là nghiệm của bất phương trình - x + 2y – 4 < 0.
Do đó, miền nghiệm của bất phương trình - x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ e, có chứa gốc O (là miền tô màu trong hình vẽ sau).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (kg) là khối lượng sản phẩm A, y (kg) là khối lượng sản phẩm B mà công ty sản xuất.
Hiển nhiên x ≥ 0 và y ≥ 0.
Số nguyên liệu loại I cần dùng để sản xuất ra x kg sản phẩm A là 2x (kg).
Số nguyên liệu loại I cần dùng để sản xuất ra y kg sản phẩm B là y (kg).
Tổng nguyên liệu loại I cần dùng là 2x + y (kg).
Mặt khác, số nguyên liệu dự trữ loại I là 8 kg, nên ta có bất phương trình : 2x + y ≤ 8.
Tương tự,
Số nguyên liệu loại II cần dùng để sản xuất ra x kg sản phẩm A là 4x (kg).
Số nguyên liệu loại II cần dùng để sản xuất ra y kg sản phẩm B là 4y (kg).
Tổng nguyên liệu loại II cần dùng là 4x + 4y (kg).
Số nguyên liệu dự trữ loại II là 24 kg, nên ta có bất phương trình : 4x + 4y ≤ 24, tức là x + y ≤ 6.
Số nguyên liệu loại III cần dùng để sản xuất ra x kg sản phẩm A là x (kg).
Số nguyên liệu loại III cần dùng để sản xuất ra y kg sản phẩm B là 2y (kg).
Tổng nguyên liệu loại III cần dùng là x + 2y (kg).
Số nguyên liệu dự trữ loại III là 8 kg, nên ta có bất phương trình : x + 2y ≤ 8.
Vậy ta có hệ bất phương trình sau :
Biểu diễn miền nghiệm của hệ này trên mặt phẳng tọa độ Oxy ta được hình sau :
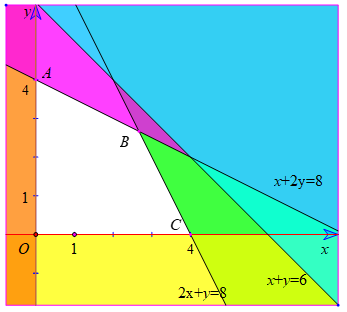
Miền nghiệm của hệ là miền tứ giác OABC (bao gồm các cạnh) với các đỉnh O(0 ; 0) ; A (0 ; 4) ; B( ; ) ; C(4 ; 0).
Gọi F là số tiền lãi thu được (đơn vị: triệu đồng), ta có:
Tiền lãi thu được từ x kg sản phẩm loại A là : 30x (triệu đồng) .
Tiền lãi thu được từ y kg sản phẩm loại B là : 50y (triệu đồng).
Khi đó F = 30x + 50y
Tính giá trị của F tại các đỉnh của tứ giác OABC :
Tại O (0 ; 0) : F = 30.0 +50.0 = 0 ;
Tại A (0 ; 4) : F = 30 . 0 + 50 . 4 = 200 ;
Tại B(; ) : F = 30 . + 50 . =
Tại C(4 ; 0) : F = 30 . 4 + 50 . 0 =120.
F đạt lớn nhất bằng 213 tại B( ; ).
Vậy công ty nên sản xuất kg sản phẩm loại A và kg sản phẩm loại B để thu về tiền lãi lớn nhất.
Lời giải
Gọi x (tấn) là khối lượng sản phẩm X mà xưởng sản xuất ra trong một ngày; y(tấn) là khối lượng sản phẩm Y mà xưởng sản xuất ra trong một ngày.
Hiển nhiên x ≥ 0 và y ≥ 0.
Để sản xuất x tấn sản phẩm X cần dùng máy A trong 6x (giờ) ; để sản xuất y tấn sản phẩm Y cần dùng máy A trong 2y (giờ).
Tổng số giờ dùng máy A trong một ngày là 6x + 2y (giờ).
Do máy A làm việc không quá 12 giờ một ngày nên ta có bất phương trình :
6x + 2y ≤ 12, hay 3x + y ≤ 6.
Để sản xuất x tấn sản phẩm X cần dùng máy B trong 2x (giờ) ; để sản xuất y tấn sản phẩm Y cần dùng máy B trong 2y (giờ).
Tổng số giờ dùng máy B trong một ngày là 2x + 2y (giờ).
Do máy B làm việc không quá 8 giờ một ngày nên ta có bất phương trình : 2x + 2y ≤ 8, hay x + y ≤ 4.
Vậy ta có hệ bất phương trình :
Biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ Oxy ta được hình sau :
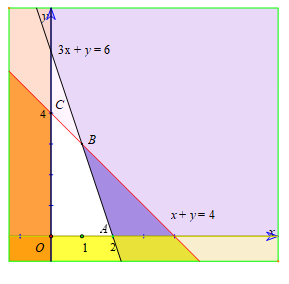
Miền nghiệm của hệ là miền tứ giác OABC (bao gồm cả các cạnh) với các đỉnh O(0 ; 0) ; A (2 ; 0) ; B(1 ; 3) ; C(0 ; 4).
Gọi F (triệu đồng) là số tiền lãi thu được.
Với x tấn sản phẩm X thì số tiền lãi là 10x (triệu đồng) ; với y tấn sản phẩm Y thì số tiền lãi là 8y (triệu đồng). Tổng số tiền lãi là 10x + 8y (triệu đồng).
Do đó F =10x + 8y
Tính giá trị của F tại các đỉnh của tứ giác OABC :
Tại O (0 ; 0): F = 10.0 + 8.0 = 0;
Tại A (2 ; 0): F= 10.2 + 8.0 = 20 ;
Tại B(1 ; 3): F = 10.1 + 8.3 = 34;
Tại C(0 ; 4): F = 10.0 + 8.4 = 32.
F đạt giá trị lớn nhất là 34 tại B(1 ; 3)
Vậy để tổng số tiền lãi cao nhất thì xưởng phải sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo