Câu hỏi:
13/07/2024 3,218
Cho đoạn thẳng AB có độ dài 20cm. Trên đoạn thẳng AB lấy hai điểm C và D sao cho AC = 6cm; AD = 12cm.
a) Tính độ dài BC; CD.
b) C có phải là trung điểm của AD không? Vì sao?
Cho đoạn thẳng AB có độ dài 20cm. Trên đoạn thẳng AB lấy hai điểm C và D sao cho AC = 6cm; AD = 12cm.
a) Tính độ dài BC; CD.
b) C có phải là trung điểm của AD không? Vì sao?
Câu hỏi trong đề: Đề kiểm tra Giữa học kì 2 Toán 6 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
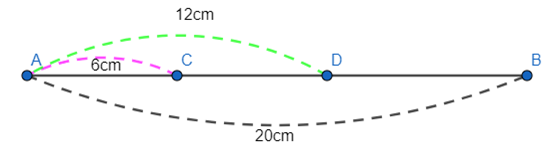
a) Vì C nằm trên đoạn thẳng AB nên AC + CB = AB
Thay số: 6 + CB = 20
CB = 20 – 6 = 14cm
Vì AC = 6cm và AD = 12 cm nên AC < AD. Do đó C nằm giữa A và D.
Ta có: AD = AC + CD
Thay số: 12 = 6 + CD
CD = 12 – 6
CD = 6cm
b) Ta có: C nằm giữa A và D.
Lại có AC = CD = \(\frac{{AD}}{2} = \frac{{12}}{2} = 6cm\)
Do đó C là trung điểm của AD
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới)
Đã bán 361
₫ 245.000
₫ 126.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Chứng minh rằng phân số \(\frac{{3n + 2}}{{5n + 3}}\) tối giản với mọi số tự nhiên n.
Xem đáp án »
13/07/2024
9,259
Câu 2:
Cho đoạn thẳng AB = 12cm. Gọi O là trung điểm của AB. Độ dài OB là:
Xem đáp án »
15/06/2022
2,220
Câu 3:
II. Tự luận
Thực hiện phép tính:
a) \(\frac{2}{{ - 9}} - \frac{5}{{ - 36}} - \frac{1}{4}\)
b) \(\left( {\frac{{ - 4}}{{ - 14}} - \frac{3}{{ - 15}}} \right) - \left( {\frac{1}{5} - \frac{{20}}{{35}} - \frac{{ - 1}}{7}} \right)\)
c) \(\frac{3}{7}.\frac{9}{{11}} + \frac{3}{7}.\frac{5}{{11}} - \frac{3}{7}.\frac{{25}}{{11}}\)
II. Tự luận
Thực hiện phép tính:
a) \(\frac{2}{{ - 9}} - \frac{5}{{ - 36}} - \frac{1}{4}\)
b) \(\left( {\frac{{ - 4}}{{ - 14}} - \frac{3}{{ - 15}}} \right) - \left( {\frac{1}{5} - \frac{{20}}{{35}} - \frac{{ - 1}}{7}} \right)\)
c) \(\frac{3}{7}.\frac{9}{{11}} + \frac{3}{7}.\frac{5}{{11}} - \frac{3}{7}.\frac{{25}}{{11}}\)
Xem đáp án »
13/07/2024
1,742
Câu 4:
Xếp loại thi đua ba tổ lao động của một đội sản xuất được thống kê như sau (đơn vị: người):
Tổ
Giỏi
Khá
Đạt
Tổ 1
8
3
1
Tổ 2
9
2
1
Tổ 3
7
4
1
a) Mỗi tổ lao động có bao nhiêu người.
b) Đội trưởng thông báo rằng số lao động giỏi của cả đội nhiều hơn số lao động khá và đạt của cả đội là 12 người. Đội trưởng thông báo đúng hay sai.
Xếp loại thi đua ba tổ lao động của một đội sản xuất được thống kê như sau (đơn vị: người):
|
Tổ |
Giỏi |
Khá |
Đạt |
|
Tổ 1 |
8 |
3 |
1 |
|
Tổ 2 |
9 |
2 |
1 |
|
Tổ 3 |
7 |
4 |
1 |
a) Mỗi tổ lao động có bao nhiêu người.
b) Đội trưởng thông báo rằng số lao động giỏi của cả đội nhiều hơn số lao động khá và đạt của cả đội là 12 người. Đội trưởng thông báo đúng hay sai.
Xem đáp án »
13/07/2024
1,451
Câu 5:
Nếu gieo một con xúc sắc 10 lần liên tiếp, có 4 lần xuất hiện mặt 5 chấm thì xác suất thực nghiệm xuất hiện mặt 5 chấm là:
Xem đáp án »
15/06/2022
1,157
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11
-
Đề thi Cuối kì học kỳ 2 Toán 6 có đáp án (Đề 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận