Bốn thửa ruộng thu hoạch được \[15\] tấn thóc. Thửa thứ nhất thu hoạch được \[\frac{7}{{20}}\] số thóc, thửa thứ hai thu hoạch được \[10\% \] số thóc, thửa thứ ba thu hoạch được \[\frac{2}{5}\] tổng số thóc thu hoạch của thửa thứ nhất và thửa thứ hai. Hỏi thửa thứ tư thu hoạch được bao nhiêu tấn thóc?

Hướng dẫn giải :

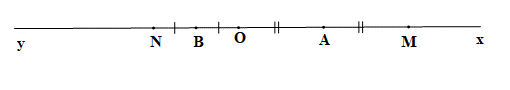
a) Vì O thuộc đường thẳng xy, mà điểm A thuộc tia Ox, điểm B thuộc tia Oy nên điểm O nằm giữa A và B.

b) Ta có A là trung điểm của OM nên \(OA = AM = \frac{{OM}}{2} = \frac{4}{2} = 2\) (cm)

Điểm B là trung điểm của ON nên \(OB = BN = \frac{{ON}}{2} = \frac{2}{2} = 1\) (cm).

Theo câu a, điểm O nằm giữa A và B nên AO + OB = AB.

Do đó AB = 2 + 1 = 3 (cm).

Vậy AB = 3 cm.

Hướng dẫn giải:

a) 34,9 – 31,5 + 58,8 – 55,4      

= (34,9 – 31,5) + (58,8 – 55,4)  

= 3,4 + 3,4

= 6,8

b) \[\frac{{ - 3}}{{31}} - \frac{6}{{17}} - \frac{{ - 1}}{{25}} + \frac{{ - 28}}{{31}} + \frac{{ - 11}}{{17}} - \frac{1}{5}\]

\[ = \frac{{ - 3}}{{31}} + \frac{{ - 28}}{{31}} - \frac{6}{{17}} + \frac{{ - 11}}{{17}} - \frac{{ - 1}}{{25}} - \frac{1}{5}\]

\[ = \left( {\frac{{ - 3}}{{31}} + \frac{{ - 28}}{{31}}} \right) + \left( { - \frac{6}{{17}} + \frac{{ - 11}}{{17}}} \right) + \left( { - \frac{{ - 1}}{{25}} - \frac{1}{5}} \right)\]

 \[ = \frac{{\left( { - 3} \right) + \left( { - 28} \right)}}{{31}} + \frac{{\left( { - 6} \right) + \left( { - 11} \right)}}{{17}} + \left( {\frac{1}{{25}} - \frac{5}{{25}}} \right)\]

\[ = \frac{{ - 31}}{{31}} + \frac{{ - 17}}{{17}} + \frac{{1 - 5}}{{25}}\]

\( = \left( { - 1} \right) + \left( { - 1} \right) + \frac{{ - 4}}{{25}}\)

\( = - 2 + \frac{{ - 4}}{{25}}\)

\( = \frac{{ - 50}}{{25}} + \frac{{ - 4}}{{25}}\)

\( = \frac{{ - 50 + \left( { - 4} \right)}}{{25}}\)

\( = \frac{{ - 54}}{{25}}.\)

c) \[2\frac{2}{9}:1\frac{1}{9} - \frac{{46}}{5}:4\frac{3}{5}\]

\[ = \frac{{20}}{9}:\frac{{10}}{9} - \frac{{46}}{5}:\frac{{23}}{5}\]

\[ = \frac{{20}}{9}.\frac{9}{{10}} - \frac{{46}}{5}.\frac{5}{{23}}\]

\( = \frac{{20.9}}{{9.10}} - \frac{{46.5}}{{5.23}}\)

= 2 – 2

= 0

d) \[\left( {4 - \frac{{12}}{{10}}} \right):2 + 30\% \]

\[ = \left( {4 - \frac{6}{5}} \right):2 + \frac{{30}}{{100}}\]

\( = \left( {\frac{{20}}{5} - \frac{6}{5}} \right):2 + \frac{3}{{10}}\)

\( = \frac{{14}}{5}.\frac{1}{2} + \frac{3}{{10}}\)

\( = \frac{{14}}{{10}} + \frac{3}{{10}}\)

\( = \frac{{17}}{{10}}\).