Câu hỏi:
13/07/2024 2,128
Cho hình chữ nhật ABCD có AB = 8 cm; BC = 6 cm. Vẽ đường cao AH của ∆ADB.
a) Chứng minh: ∆AHB đồng dạng ∆BCD.
b) Chứng minh: AD2 = DH . DB.
c) Tính độ dài đoạn thẳng AH.
Cho hình chữ nhật ABCD có AB = 8 cm; BC = 6 cm. Vẽ đường cao AH của ∆ADB.
a) Chứng minh: ∆AHB đồng dạng ∆BCD.
b) Chứng minh: AD2 = DH . DB.
c) Tính độ dài đoạn thẳng AH.
Câu hỏi trong đề:
Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
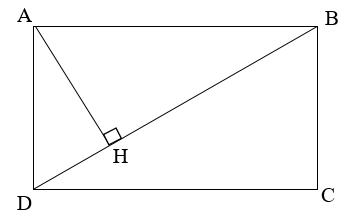
a) Vì ABCD là hình chữ nhật nên AB // CD.
Suy ra: (hai góc so le trong).
Xét ∆AHB và ∆BCD có:
(cmt).
Do đó ∆AHB 
∆BCD (g.g).
b) Xét ∆AHD và ∆BAD có:
chung.
Do đó ∆AHD ∆BAD (g.g)
Suy ra .
Vậy AD2 = DH . BD (đpcm).
c) Xét ∆ABD vuông tại A, áp dụng định lý Py-ta-go, ta có:
BD2 = AB2 + AD2 = 82 + 62 = 100
Suy ra: BD = 10 (cm)
Từ câu a: ∆AHB ∆BCD suy ra .
Hay AH . BD = AB. BC.
Do đó (cm).
Vậy AH = 4,8 cm.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
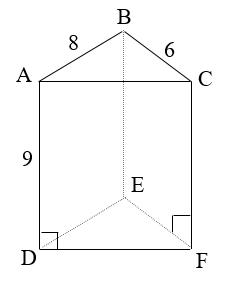
Cho hình lăng trụ đứng ABC.DEF (như hình vẽ) có đáy là tam giác vuông, biết độ dài hai cạnh góc vuông là 6 cm và 8 cm; chiều cao của lăng trụ là 9 cm. Tính diện tích toàn phần của hình lăng trụ?
Xem đáp án »
13/07/2024
3,650
Câu 2:
Một vòi nước chảy vào bể không có nước. Cùng lúc đó một vòi nước khác chảy từ bể ra. Mỗi giờ lượng nước vòi chảy ra bằng 
lượng nước chảy vào. Sau 5 giờ thì bên trong bể đạt tới 
dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu thì đầy bể?
Một vòi nước chảy vào bể không có nước. Cùng lúc đó một vòi nước khác chảy từ bể ra. Mỗi giờ lượng nước vòi chảy ra bằng lượng nước chảy vào. Sau 5 giờ thì bên trong bể đạt tới dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu thì đầy bể?
Xem đáp án »
13/07/2024
877
Câu 4:
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
Xem đáp án »
20/06/2022
627
Câu 5:
Giải các phương trình và bất phương trình sau:
a) (x – 2)(x + 7) = 0;
b) .
Giải các phương trình và bất phương trình sau:
a) (x – 2)(x + 7) = 0;
b) .
Xem đáp án »
13/07/2024
614
Bình luận
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
15 câu Trắc nghiệm Toán 8 KNTT Bài 1: Đơn thức có đáp án
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
10 Bài tập Bài toán thực tiễn liên quan đến thể tích, diện tích xung quanh của hình chóp tứ giác đều (có lời giải)
-
Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
về câu hỏi!