Cho hình bình hành ABCD và điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chứng minh:

a) Chứng minh: ∆DEA  ∆BEF và ∆DGE ∆BAE.

b) Chứng minh: AE² = EF . EG.

c) Chứng minh rằng BF. DG không đổi khi điểm F thay đổi trên BC.

Gọi x (km/h) vận tốc của tàu khi nước yên lặng (x > 4).

Đổi: 8 giờ 20 phút = $\frac{25}{3}$ giờ.

Vận tốc của tàu khi xuôi dòng là: x + 4 (km/h).

Vận tốc của tàu khi ngược dòng là: x − 4 (km/h).

Thời gian tàu đi xuôi dòng là: $\frac{80}{x+4}$ (giờ).

Thời gian tàu đi ngược dòng là: $\frac{80}{x-4}$ (giờ).

Vì thời gian cả đi lẫn về là 8 giờ 20 phút hay $\frac{25}{3}$ giờ nên ta có phương trình:

$\frac{80}{x+4}+\frac{80}{x-4}=\frac{25}{3}$

$\iff \frac{16}{x+4}+\frac{16}{x-4}=\frac{5}{3}$

$\iff \frac{48(x-4)}{3(x+4)(x-4)}+\frac{48(x+4)}{3(x+4)(x-4)}=\frac{5(x+4)(x-4)}{3(x+4)(x-4)}$

$\Rightarrow$ 48(x – 4) + 48(x + 4) = 5(x + 4)(x – 4)

Û 48(x – 4 + x + 4) = 5(x² – 16)

Û 96x = 5x² – 80

Û 5x² – 96x – 80 = 0

Û (x – 20)(5x + 4) = 0

Û x = 20 (TM) hoặc $x=\frac{-4}{5}$ (loại)

Vậy vận tốc của tàu khi nước yên lặng là 20 km/h.

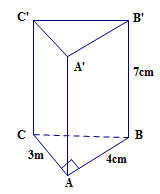
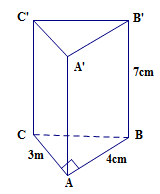
Áp dụng định lí Py-ta-go vào ∆ABC vuông tại A, ta có:

BC² = AB² + AC² = 3² + 4² = 25.

Suy ra: BC = 5 cm.

Ta có: S_xq = (AB +AC + BC) . BB’

= (3 + 4 + 5) . 7 = 84 (cm²).

Vậy diện tích xung quanh của hình lăng trụ là 84 cm².