Câu hỏi:
21/06/2022 670Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H, K. So sánh BH và CK.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
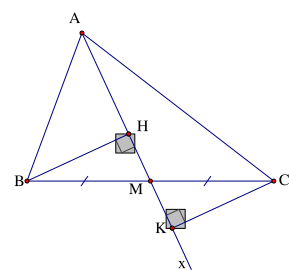
Xét \[\Delta BHM\] và \[\Delta CKM\] có:
\[\widehat {BHM} = \widehat {CKM}\,( = {90^{\rm{o}}})\]
BM = CM (Vì M là trung điểm cạnh BC)
\[\widehat {BMH} = \widehat {CMK}\] (hai góc đối đỉnh)
⇒ \[\Delta BHM = \Delta CKM\] (cạnh huyền – góc nhọn)
Suy ra BH = CK (hai cạnh tương ứng)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
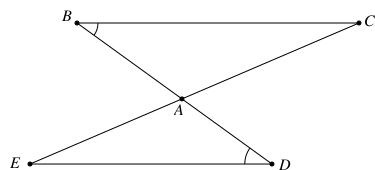
Xét tam giác ABC và tam giác ADE có:
\(\widehat B = \widehat D\)
\(\widehat {BAC} = \widehat {DAE}\) (2 góc đối đỉnh)
Mà \(\widehat B\) và \(\widehat {BAC}\) là hai góc kề của cạnh AB; \(\widehat D\) và \(\widehat {DAE}\) là hai góc kề của cạnh AD
Vậy để 2 tam giác bằng nhau theo trường hợp g.c.g cần có thêm điều kiện AB = AD.
Lời giải
Đáp án đúng là: A
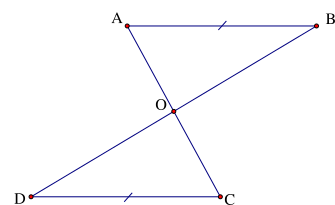
Xét \[\Delta AOB\] và \[\Delta COD\] có:
\(\widehat {OAB} = \widehat {OCD}\) (2 góc so le trong do \(AB{\rm{//}}CD\))
AB = CD (gt)
\(\widehat {OBA} = \widehat {ODC}\) (2 góc so le trong do \(AB{\rm{//}}CD\))
\[ \Rightarrow \Delta AOB = \Delta COD\] (g.c.g)
Suy ra OA = OC (hai cạnh tương ứng)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2