Câu hỏi:
12/07/2024 1,929
Cho ΔABC cân tại A kẻ AH\[ \bot \]BC (H\[ \in \]BC).
a) Chứng minh: HB = HC.
b) Kẻ HD\[ \bot \]AB (D\[ \in \]AB), HE\[ \bot \]AC (E\[ \in \]AC). Chứng minh ΔHDE cân.
c) Cho \(\widehat {BAC} = {120^o}\) thì ΔHDE trở thành tam giác gì? Vì sao?
Cho ΔABC cân tại A kẻ AH\[ \bot \]BC (H\[ \in \]BC).
a) Chứng minh: HB = HC.
b) Kẻ HD\[ \bot \]AB (D\[ \in \]AB), HE\[ \bot \]AC (E\[ \in \]AC). Chứng minh ΔHDE cân.
c) Cho \(\widehat {BAC} = {120^o}\) thì ΔHDE trở thành tam giác gì? Vì sao?
Câu hỏi trong đề: Đề kiểm tra Giữa kì 2 Toán 7 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
GT |
ΔABC cân tại A; AH\[ \bot \]BC (H\[ \in \]BC); HD\[ \bot \]AB (D\[ \in \]AB), HE\[ \bot \]AC (E\[ \in \]AC). |
|
KL |
a) Chứng minh: HB = HC. b) ΔHDE cân. c) Cho \(\widehat {BAC} = {120^o}\) thì ΔHDE trở thành tam giác gì? Vì sao? |
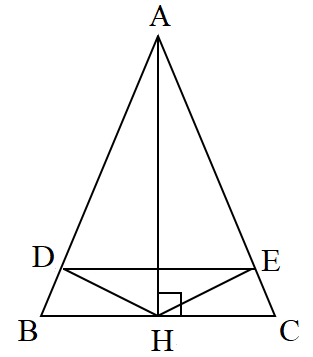
a) Xét ΔABC cân tại A có AH là đường cao (vì AH\[ \bot \]BC) nên AH cũng là đường trung tuyến.
Do đó HB = HC.
b) Xét ΔBDH vuông tại D và ΔCEH vuông tại E có:
HB = HC (cmt)
\(\widehat B = \widehat C\) (ΔABC cân tại A)
Do đó ΔBDH = ΔCEH (cạnh huyền - góc nhọn).
Suy ra DH = HE (hai cạnh tương ứng)
Suy ra ΔHDE cân tại H.
Mặt khác, vì \(\widehat A = {120^o}\) nên \(\widehat B = \widehat C = \frac{1}{2}\,.\,({180^o} - \widehat A) = \frac{1}{2}\,.\,{60^o} = {30^o}\).
Từ ΔBDH = ΔCEH (cmt) suy ra \(\widehat {BHD} = \widehat {CHE}\) (hai góc tương ứng).
Xét ΔBDH vuông tại D nên \(\widehat B + \widehat {BHD} = {90^o} \Rightarrow \widehat {BHD} = {90^o} - \widehat B = {60^o}\).
Do đó \(\widehat {BHD} = \widehat {CHE} = {60^o}\)
Ta có:\(\widehat {BHC} = \widehat {BHD} + \widehat {DHE} + \widehat {EHC}\)
Suy ra \(\widehat {DHE} = \widehat {BHC} - \left( {\widehat {BHD} + \widehat {CHE}} \right)\)
\( \Rightarrow \widehat {AHE} = {180^o} - ({60^o} + {60^o}) = {60^o}\).
Ta thấy ΔHED cân tại H có \(\widehat {AHE} = {60^o}\)nên ΔHED là tam giác đều.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Dấu hiệu: Điểm kiểm tra môn toán của mỗi học sinh lớp 7A.
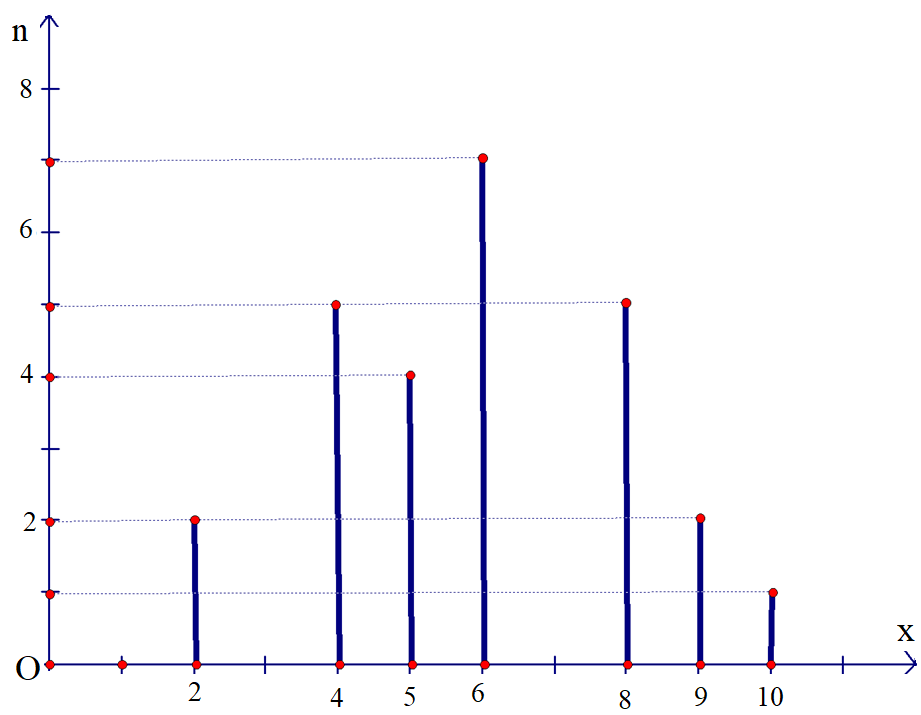
b) Bảng “tần số”:
|
Điểm (x) |
2 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số (n) |
2 |
5 |
4 |
7 |
6 |
5 |
2 |
1 |
N = 32 |
* Nhận xét:
- Số các giá trị của dấu hiệu: 32.
- Số các giá trị khác nhau của dấu hiệu: 9.
- Điểm kiểm tra cao nhất: 10 điểm
- Điểm kiểm tra thấp nhất: 2 điểm
- Đa số học sinh được điểm từ 7 đến 9.
c)
* Số trung bình cộng:
\(\overline X = \frac{{2\,.\,2 + 4\,.\,5 + 5\,.\,4 + 6\,.\,7 + 7\,.\,6 + 8\,.\,5 + 9\,.\,2 + 10\,.\,1}}{{32}} = \frac{{196}}{{32}} = 6,125\) (điểm).
* Mốt của dấu hiệu: M0 = 7
d) Biểu đồ đoạn thẳng:
Lời giải
Thay x = 1 vào đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\), ta được:
\(f(1) = \frac{2}{3}\,.\,1 - 1 = - \frac{1}{3} \ne \frac{1}{3}\).
Do đó, điểm \(A\left( {1;\,\,\frac{1}{3}} \right)\) không thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Và điểm \(B\left( {1;\,\, - \frac{1}{3}} \right)\) thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Thay x = −3 vào đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\), ta được:
\(f( - 3) = \frac{2}{3}\,.\,( - 3) - 1 = - 3 \ne 1\).
Do đó, điểm C(−3; 1) không thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Thay x = 6 vào đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\), ta được:
\(f(6) = \frac{2}{3}\,.\,6 - 1 = 3 \ne - 3\).
Do đó, điểm D(6; −3) không thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Vậy chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 02
-
Đề thi giữa học kì 2 Toán 7 KNTT - Đề 01 có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận