Cho tam giác ABC. Ở phía ngoài tam giác đó vẽ các tam giác vuông cân tại A là ABD và ACE.
a) Chứng minh CD = BE và CD vuông góc với BE;
b) Lấy điểm K nằm trong tam giác ABD sao cho góc ABK bằng 300, BA = BK. Chứng minh: AK = KD.
Cho tam giác ABC. Ở phía ngoài tam giác đó vẽ các tam giác vuông cân tại A là ABD và ACE.
a) Chứng minh CD = BE và CD vuông góc với BE;
b) Lấy điểm K nằm trong tam giác ABD sao cho góc ABK bằng 300, BA = BK. Chứng minh: AK = KD.
Câu hỏi trong đề: Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
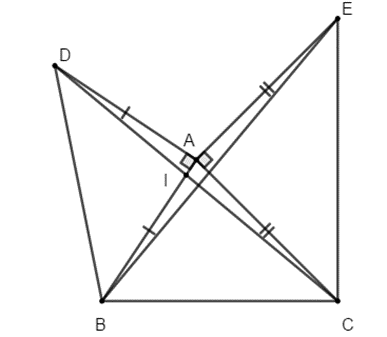
-Vẽ hình đúng được 0,5 điểm. (sai hình không chấm)
a) Xét tam giác ADC và tam giác ABE có:
AD = AB (Tam giác ADB cân tại A)
AC = AE (Tam giác ACE vuông tại A)
Do đó:
Suy ra DC = BE (2 cạnh tương ứng); (2 góc tương ứng)
Gọi I là giao điểm của DC và AB.
Ta có: (đối đỉnh); (c/m trên)
Mà (tam giác IAD vuông tại A) suy ra
Suy ra DC vuông góc với BE. (1 điểm)
b)
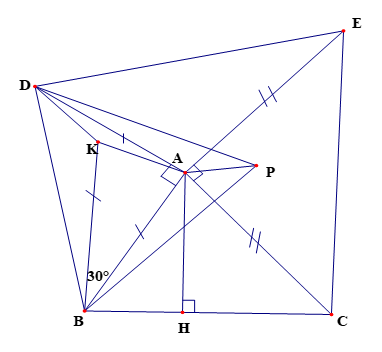
Vẽ tam giác đều BPD sao cho P và A nằm cùng phía đối với BD
Ta có: suy ra
Suy ra suy ra (1)
Tam giác BAK cân tại B có góc ABK = 300
Nên suy ra (2)
Từ (1) và (2) suy ra: nên tam giác KDA cân tại K suy ra KA = KD (1 điểm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
D. 2cm, 3cm, 5cm
Lời giải
+ Ta có: 2 + 4 = 6 nên bộ ba số 2cm, 4cm, 6cm không phải là độ dài ba cạnh của một tam giác.
+ Có 2 + 4 = 6 < 7 nên bộ ba số 2cm, 4cm, 7cm không phải độ dài ba cạnh của tam giác.
+ Ta có: 3 + 4 = 7 > 5; 3 + 5 = 8 > 4 và 4 + 5 = 9 > 3 nên bộ ba số 3cm, 4cm, 5 cm là độ dài ba cạnh của một tam giác.
+ Vì 2 + 3 = 5 nên bộ ba số 2cm, 3cm, 5 cm không phải độ dài ba cạnh của một tam giác.
Chọn đáp án C
Câu 2
D. BD < BC < AB
Lời giải
Cho hình vẽ bên. So sánh AB, BC, BD ta được:
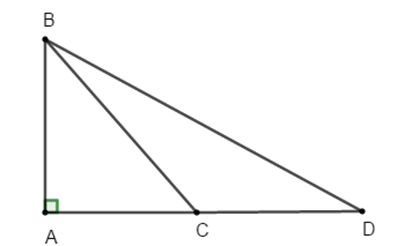
Vì BA AD và C nằm giữa A và D nên AC < AD
Do đó: AB < BC < BD (quan hệ đường xiên và hình chiếu).
Chọn đáp án A
Câu 3
D. AG = AM
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
B. AC > AB > BC
D. BC > AC > AB
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
B. Đường phân giác.
D. Đường trung trực
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.