Câu hỏi:
11/07/2024 617
Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.
a) So sánh góc ADC và góc AEB;
b) So sánh các đoạn thẳng AD và AE.
Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.
a) So sánh góc ADC và góc AEB;
b) So sánh các đoạn thẳng AD và AE.
Câu hỏi trong đề:
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) !!
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vẽ hình đúng, ghi GT-KL được 0,5 điểm.
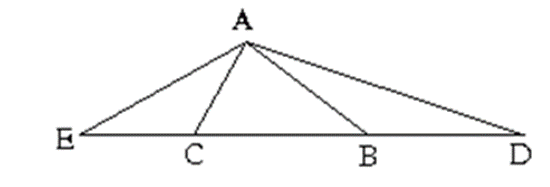
a) ΔACB có AC < AB góc ACB > góc ABC
=> góc ACE < góc ABD (1) (Vì góc ACB; góc ACE kề bù và góc ABD; góc ABC kề bù)
Xét tam giác cân ACE đáy AE (vì AC = CE) và tam giác ABD cân tại B (vì AB = BD) ta có: 2ˆE+^ACE=2ˆD+^ABD (=180°) (2).
Từ (1) và (2) ⇒^ADC<^AEBb, Xét tam giác ADE có ^ADC<^AEB⇒AD>AE
Nhà sách vietjack
- Trọng tâm Toán, Anh, KHTN lớp 7 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 60.000₫ )
- Sổ Takenote Ngữ văn 7 Kết Nối Tri Thức, Chân Trời, Cánh Diều VietJack ( 38.000₫ )
- Combo 2 sách Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 cho cả 3 bộ KNTT; CTST; CD VietJack ( 120.000₫ )
- Sách Lớp 9 - Siêu trọng tâm Toán, Văn, Anh VietJack ( 97.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC với AD là trung tuyến, G là trọng tâm, AD = 12 cm. Khi đó độ dài đoạn GD bằng:
Cho tam giác ABC với AD là trung tuyến, G là trọng tâm, AD = 12 cm. Khi đó độ dài đoạn GD bằng:
Xem đáp án »
26/06/2022
1,127
Câu 3:
a) Tìm nghiệm của đa thức: P(y)=12y+3
b) Chứng tỏ đa thức sau không có nghiệm: .
a) Tìm nghiệm của đa thức: P(y)=12y+3
b) Chứng tỏ đa thức sau không có nghiệm: .
Xem đáp án »
26/06/2022
272
Câu 4:
Câu 1: Thực hiện phép tính: (34xy3)(−65x2y2) ta được kết quả bằng:
Câu 1: Thực hiện phép tính: (34xy3)(−65x2y2) ta được kết quả bằng:
Xem đáp án »
26/06/2022
263
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 01
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 01
-
12 Bài tập Một số bài toán thực tế liên quan đại lượng tỉ lệ thuận (có lời giải)
-
12 Bài tập Một số bài toán thực tế liên quan đại lượng tỉ lệ nghịch (có lời giải)
-
Bộ 5 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 02
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận