Chọn vé tàu (H.8.2)

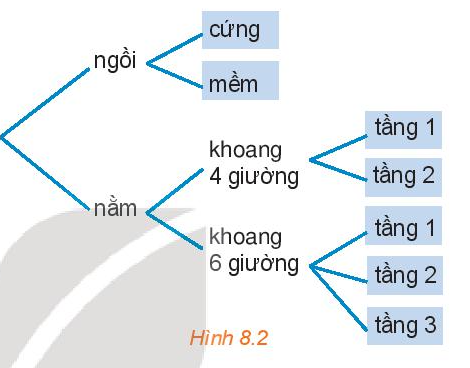
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có hai loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại khoang 4 giường và khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2 và tầng 3. Hỏi:

a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?

b) Có bao nhiêu loại vé để bạn An lựa chọn?

Hướng dẫn giải

a) Gọi số tự nhiên cần lập có dạng: \(\overline {abc} \), với a, b, c thuộc tập hợp số A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}, (a ≠ 0, a ≠ b ≠ c).

Để lập số này, ta thực hiện ba công đoạn liên tiếp:

+ Chọn số a có 9 cách, do a ≠ 0.

+ Chọn b có 9 cách từ tập A\{a}.

+ Chọn c có 8 cách từ tập A\{a; b}.

Vậy số các số tự nhiên có 3 chữ số khác nhau là: 9 . 9 . 8 = 648 (số).

b) Gọi số tự nhiên cần lập có dạng: \(\overline {abc} \), với a, b, c thuộc tập hợp số A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}, (a ≠ 0, a ≠ b ≠ c).

Để \(\overline {abc} \) là số lẻ thì c thuộc tập hợp {1; 3; 5; 7; 9},

+ Chọn c có 5 cách từ tập {1; 3; 5; 7; 9}.

+ Chọn a có 8 cách từ tập A\{c; 0}.

+ Chọn b có 8 cách từ tập A\{c; a}.

Vậy số các số tự nhiên là số lẻ có 3 chữ số khác nhau là: 5 . 8 . 8 = 320 (số).

c) Gọi số tự nhiên cần lập có dạng: \(\overline {abc} \), với a, b, c thuộc tập hợp số A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}, (a ≠ 0).

Để \(\overline {abc} \)chia hết cho 5 thì c thuộc tập hợp {0; 5}.

+ Chọn c có 2 cách từ tập {0; 5}.

+ Chọn a có 9 cách từ tập A\{0}.

+ Chọn b có 10 cách từ tập A.

Vậy số các số tự nhiên có 3 chữ số mà chia hết cho 5 là: 2 . 9 . 10 = 180 (số).

d) Gọi số tự nhiên cần lập có dạng: \(\overline {abc} \), với a, b, c thuộc tập hợp số A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}, (a ≠ 0, a ≠ b ≠ c).

Để \(\overline {abc} \) chia hết cho 5 thì c thuộc tập hợp {0; 5}.

+ Trường hợp 1: Nếu c = 0 thì: chọn a có 9 cách, chọn b có 8 cách.

Do đó, số các số tự nhiên có 3 chữ số khác nhau mà tận cùng là 0 là: 9 . 8 = 72 (số).

+ Trường hợp 2: Nếu c = 5 thì: chọn a có 8 cách (do a ≠ 0 và a ≠ c), chọn b có 8 cách (do a ≠ b ≠ c).

Do đó, số các số tự nhiên có 3 chữ số khác nhau mà tận cùng là 5 là: 8 . 8 = 64 (số).

Vì hai trường hợp rời nhau nên ta áp dụng quy tắc cộng, vậy số các số tự nhiên có 3 chữ số khác nhau mà chia hết cho 5 là: 72 + 64 = 136 (số).

Hướng dẫn giải

a) Để lập một mật khẩu chương trình máy tính, ta cần thực hiện ba công đoạn liên tiếp:

+ Chọn kí tự thứ nhất: có 10 cách chọn (chọn 1 chữ số trong 10 chữ số từ 0 đến 9).

+ Chọn kí tự thứ hai: tương tự kí tự thứ nhất, có 10 cách chọn.

+ Chọn kí tự thứ ba: tương tự trên, có 10 cách chọn.

Vậy theo quy tắc nhân, có thể tạo được số mật khẩu là: 10 . 10 . 10 = 1 000 (mật khẩu).

b) Để lập một mật khẩu chương trình máy tính theo quy định mới, ta cần thực hiện ba công đoạn liên tiếp:

+ Chọn kí tự thứ nhất từ tập 26 chữ từ A đến Z: có 26 cách chọn.

+ Chọn kí tự thứ hai là chữ số: có 10 cách chọn.

+ Chọn kí tự thứ ba là chữ số: có 10 cách chọn.

Do đó, theo quy tắc nhân, số cách tạo mật khẩu mới là: 26 . 10 . 10 = 2 600 (mật khẩu).

Vậy có thể tạo được nhiều hơn quy định cũ số mật khẩu là: 2 600 – 1 000 = 1 600 (mật khẩu).