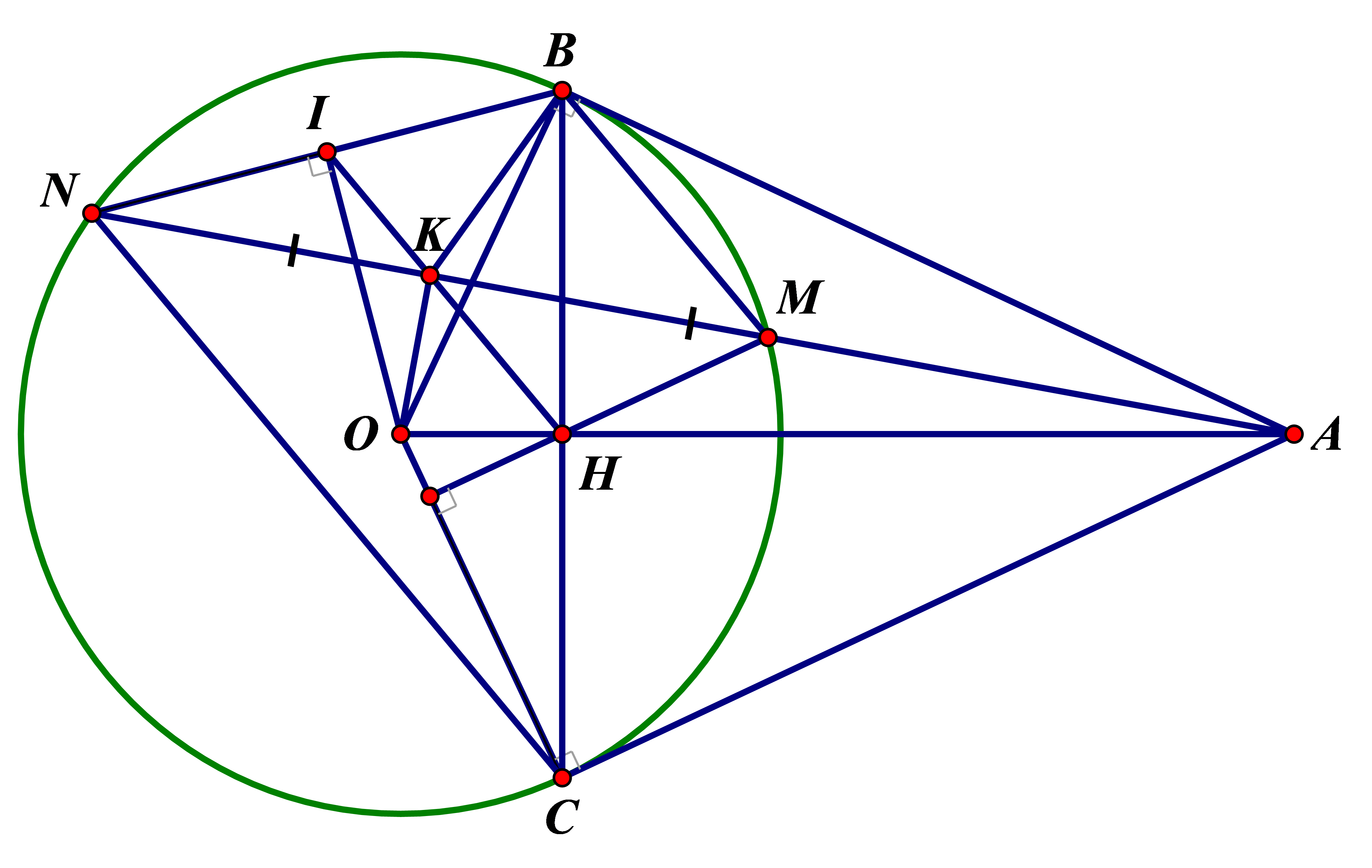
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC, qua H kẻ một đường thẳng vuông góc với OC cắt (O) tại M (M thuộc cung nhỏ BC), AM cắt (O) tại N (N khác M); gọi K là trung điểm MN.
a) Chứng minh tứ giác ABOC nội tiếp và AB.BM = AM.NB.
b) Chứng minh 5 điểm A, B, K, O, C cùng thuộc 1 đường tròn và .
c) Kẻ OI vuông góc NB tại I. Chứng minh: I, K, H thẳng hàng.
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là 2 tiếp điểm). Gọi H là giao điểm của OA và BC, qua H kẻ một đường thẳng vuông góc với OC cắt (O) tại M (M thuộc cung nhỏ BC), AM cắt (O) tại N (N khác M); gọi K là trung điểm MN.
a) Chứng minh tứ giác ABOC nội tiếp và AB.BM = AM.NB.
b) Chứng minh 5 điểm A, B, K, O, C cùng thuộc 1 đường tròn và .
c) Kẻ OI vuông góc NB tại I. Chứng minh: I, K, H thẳng hàng.
Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có:
= 90° (AB là tiếp tuyến của (O)).
= 90° (AC là tiếp tuyến của (O)).
Xét tứ giác ABOC có += 90° + 90° = 180°.
Suy ra tứ giác ABOC nội tiếp.
Xét ∆ ABM và ∆ ANB có:
là góc chung.
(Góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung BM).
Suy ra ∆ABM đồng dạng ∆ANB (g.g)
Từ đó suy ra AB.BM = AM.NB (đpcm)
b) Tứ giác ABOC nội tiếp có = 90° suy ra OA là đường kính cũng suy ra tứ giác ABOC nội tiếp đường tròn đường kính OA.
Ta có OK ⊥ MN (tính chất đường kính đi qua trung điểm dây cung thì vuông góc với dây đó).
Suy ra 90° dẫn đến K thuộc đường tròn đường kính OA.
Vậy 5 điểm A, B, C, O, K cùng thuộc 1 đường tròn đường kính OA.
Vì ∆ABM 
∆ANB (cmt) nên ta có:
Û AB2 = AM.AN.
Mà ta cũng có AB2 = AH.AO (∆ ABO vuông tại B có đường cao BH).
Suy ra AM.AN = AH.AO Û .
Xét ∆AMH và ∆AON có:
là góc chung
(cmt)
Suy ra ∆AMH đồng dạng ∆AON (c.g.c)
Từ đó suy ra (hai góc tương ứng).
c) Ta có MH // AC (cùng vuông góc với OC).
Suy ra (hai góc đồng vị).
Ta lại có (tứ giác KBAC nội tiếp)
Từ đó suy ra suy ra tứ giác KBMH nội tiếp.
(tứ giác KBMH nội tiếp)
(tứ giác NBMC nội tiếp đường tròn (O))
⇒⇒ KH//NC (1)
Ta có H là trung điểm BC (tính chất hai tiếp tuyến cắt nhau).
I là trung điểm NB (đường kính vuông góc với dây cung thì đi qua trung điểm của dây).
⇒ IH là đường trung bình của tam giác NBC ⇒ IH // NC (2)
Từ (1) và (2) suy ra K, H, I thẳng hàng (theo tiên đề Ơ-clit).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Bảng giá trị:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
y = x2 |
4 |
1 |
0 |
1 |
4 |
Trên mặt phẳng tọa độ lấy các điểm A(–2; 4); B(–1; 1); O(0; 0); C(1; 1); D(2; 4).
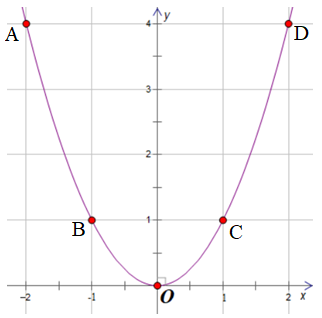
b) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = –x + 2
Û x2 + x – 2 = 0
Û x2 + 2x – x – 2 = 0
Û x( x + 2) – (x + 2) = 0
Û (x – 1)(x + 2) = 0
Û
• Với x = 1 thì y = –x + 2 = –1 + 2 = 1.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(1; 1).
• Với x = –2 thì y = –x + 2 = –(–2) + 2 = 4.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(–2; 4).
Vậy hai đồ thị hàm số trên có 2 giao điểm là A(1;1) và B(–2; 4).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Ta có: ∆ = m2 – 4.2.(–5) = m2 + 40
Vì ∆ = m2 + 40 > 0 (đúng với mọi giá trị của m).
Nên phương trình (1) luôn có 2 nghiệm với mọi m (điều phải chứng minh).
b) A = x12 – x1 + x22 – x2
= (x12 + x22) – (x1 + x2)
= (x1 + x2)2 – 2x1.x2 – (x1 + x2) (2)
Theo hệ thức Vi-et, ta có:
Thay vào (2) ta được:
A = =.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập