Cho (O;R), AB là dây cung của đường (O) sao cho AB = R3. M là một điểm trên cung lớn AB. Số đo cung AMB⌢là bao nhiêu? A. 30° B. 60° C. 45° D. 240°

Đáp án đúng là: D Kẻ OH vuông góc AB (H∈BC). Ta có: H là trung điểm AB (đường kính vuông góc dây cung thì đi qua trung điểm của dây) Suy ra AH = AB2=32R. sin AOH^ = AHAO=32.RR=32⇒ AOH^= 60°. Ta có: OA = OB = R. Suy ra tam giác OAB cân. Tam giác OAB có OH là đường cao suy ra OH cũng là đường phân giác Do đó AOB^=2AOH^=2. 60° = 120°. Số đo cung AB⌢nhỏ =AOB^= 120°. Số đo cung AMB⌢ = 360° − Số đo cung AB⌢nhỏ = 360 – 120 = 240°.

Câu hỏi:

29/06/2022 556

Cho (O;R), AB là dây cung của đường (O) sao cho AB = $R \sqrt{3}$ . M là một điểm trên cung lớn AB. Số đo cung $\overset{⌢}{A M B}$ là bao nhiêu?

A. 30°

B. 60°

C. 45°

D. 240°

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra giữa học kì 2 môn Toán 9 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: D

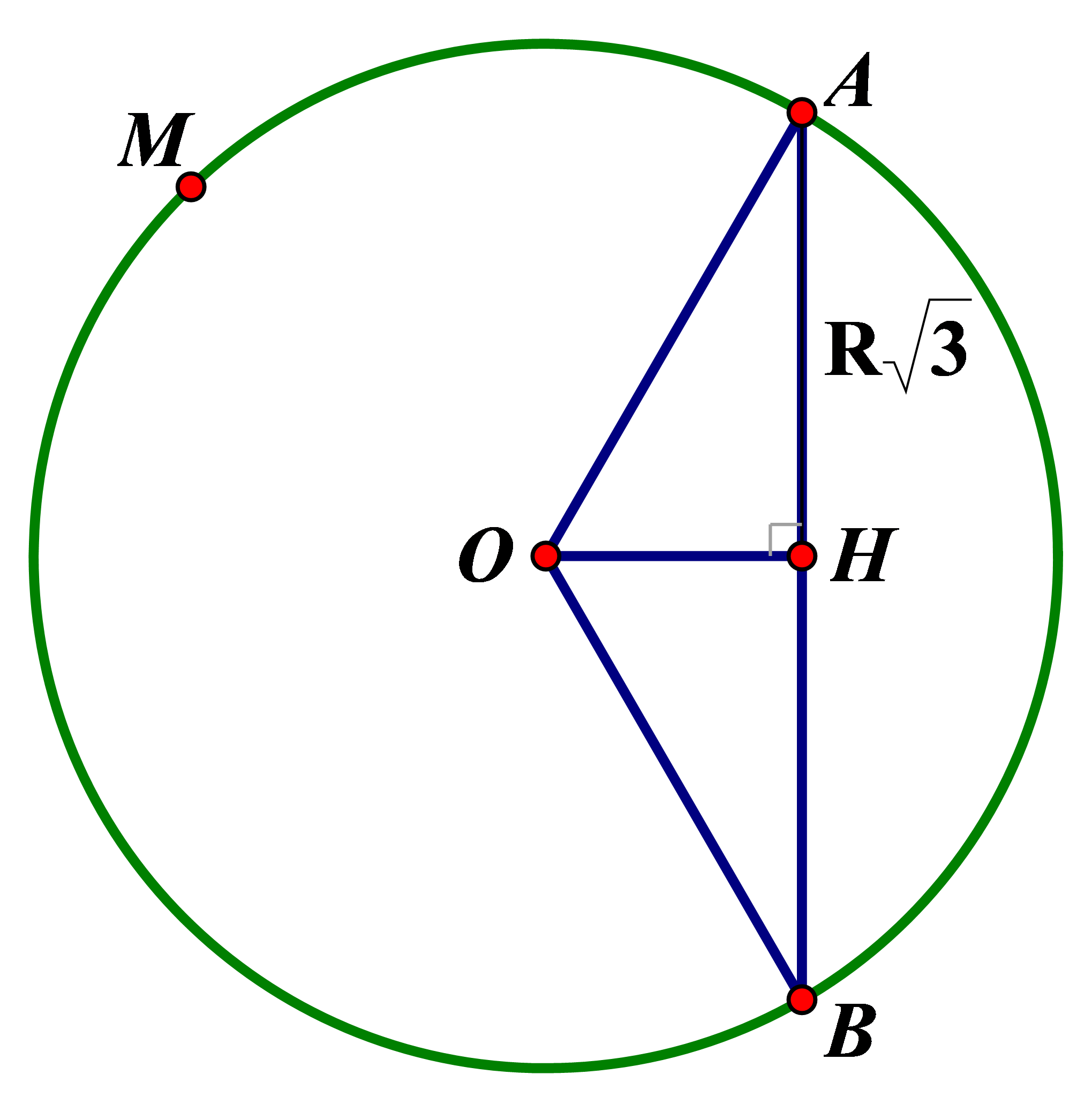
Cho (O;R), AB là dây cung của đường (O) sao cho AB = R căn 3 . M là một điểm trên cung lớn AB. Số đo cung AMB là bao nhiêu? (ảnh 1)

Kẻ OH vuông góc AB ( $H \in B C$ ).

Ta có:

H là trung điểm AB (đường kính vuông góc dây cung thì đi qua trung điểm của dây)

Suy ra AH = $\frac{A B}{2} = \frac{\sqrt{3}}{2} R$ .

sin $\hat{A O H}$ = $\frac{A H}{A O} = \frac{\sqrt{3}}{2} . \frac{R}{R} = \frac{\sqrt{3}}{2}$ ⇒ $\hat{A O H}$ = 60°.

Ta có: OA = OB = R.

Suy ra tam giác OAB cân.

Tam giác OAB có OH là đường cao suy ra OH cũng là đường phân giác

Do đó $\hat{A O B} = 2 \hat{A O H} =$ 2. 60° = 120°.

Số đo cung $\overset{⌢}{A B}$ nhỏ = $\hat{A O B}$ = 120°.

Số đo cung $\overset{⌢}{A M B}$ = 360° − Số đo cung $\overset{⌢}{A B}$ nhỏ = 360 – 120 = 240°.

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là tiếp điểm) và cát tuyến AMN không qua O (M nằm giữa A và N). Gọi H là giao điểm của OA và BC. Chứng minh rằng.

a. Tứ giác ABOC nội tiếp.

b. OA ⊥ BC

c. AB² = AM.AN

d. $\hat{A M H} = \hat{A O N}$

Xem đáp án

Lời giải

Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Qua điểm A vẽ hai tiếp tuyến AB, AC đến (O) (B, C là tiếp điểm) và cát tuyến AMN không qua O (M nằm giữa A và N). Gọi H là giao điểm của OA và BC. Chứng minh rằng. (ảnh 1)

a. Ta có:

$\hat{OBA}$ = 90° (AB là tiếp tuyến của (O))

$\hat{OCA}$ = 90° (AC là tiếp tuyến của (O))

Xét tứ giác ABOC có $\hat{OBA}$ + $\hat{OCA}$ = 90° + 90° = 180°

Suy ra tứ giác ABOC nội tiếp.

b. Ta có:

AB = AC (tính chất hai tiếp tuyến cắt nhau)

OB = OC = R.

Suy ra OA là đường trung trực của BC dẫn đến OA vuông góc BC.

c. Xét ∆ ABM và ∆ ANB có:

$\hat{NAB}$ là góc chung

$\hat{ANB} = \hat{ABM}$ (Góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung BM)

Suy ra ∆ ABM ∆ ANB (g.g)

Từ đó suy ra $\frac{A B}{A N} = \frac{A M}{A B} \Leftrightarrow A B^{2} = A M . A N$ (điều phải chứng minh)

d. ∆ ABM đồng dạng ∆ ANB (cmt) nên ta có:

AB² = AM.AN

Mà ta cũng có AB² = AH.AO (∆ ABO vuông tại B có đường cao BH)

Suy ra AM.AN = AH.AO Û $\frac{A M}{A O} = \frac{A H}{A N}$

Xét ∆ AMH và ∆ AON có:

$\hat{OAN}$ là góc chung

$\frac{A M}{A O} = \frac{A H}{A N}$ (cmt)

Suy ra ∆ AMH ∆ AON (c.g.c)

Từ đó suy ra $\hat{A M H} = \hat{A O N}$ (hai góc tương ứng).

Câu 2

Giá trị nào của a thì đồ thị hàm số y = ax² đi qua điểm (−1; 2)?

A. 2

B. −2

C. $\frac{1}{4}$

D. $\frac{- 1}{4}$

Lời giải

Đáp án đúng là: A

Thay giá trị của điểm (−1; 2) vào đổ thì hàm số y = ax² ta được:

2 = a.(−1)² Û 2 = a.

Câu 3

Cặp số (x; y) nào sau đây là nghiệm của hệ phương trình ${\begin{cases} x + 3 y = 5 \\ 2 x - y = 3 \end{cases}$

A. (2; 1)

B. (1; 2)

C. (−2; 1)

D. (1; −2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tọa độ giao điểm của hai đường thẳng y = 2x – 3 và y = x – 1 là:

A. (−2; 1)

B. (1; 2)

C. (2; 1)

D. (1; −2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Hàm số y = (m − 1)x² đồng biến với x < 0 khi:

A. m = 1

B. m > 1

C. m < 1

D. m ≠ 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Hai tủ sách có 450 quyển sách, nếu chuyển 50 quyển từ tủ một sang tủ hai thì hai tủ có số sách bằng nhau. Số sách của tủ một là:

A. 200

B. 250

C. 275

D. 300

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Điểm A thuộc nửa đường tròn (O;6cm) đường kính BC sao cho diện tích ΔABC lớn nhất. Khi đó số đo cung $\overset{⌢}{A C}$ là:

A. 120°

B. 90°

C. 60°

D. 45°

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho (O;R), AB là dây cung của đường (O) sao cho AB = R3. M là một điểm trên cung lớn AB. Số đo cung AMB⌢là bao nhiêu?

Bình luận

Giá trị nào của a thì đồ thị hàm số y = ax2 đi qua điểm (−1; 2)?

Cặp số (x; y) nào sau đây là nghiệm của hệ phương trình {x+3y=52x−y=3

Tọa độ giao điểm của hai đường thẳng y = 2x – 3 và y = x – 1 là:

Hàm số y = (m − 1)x2 đồng biến với x < 0 khi:

Hai tủ sách có 450 quyển sách, nếu chuyển 50 quyển từ tủ một sang tủ hai thì hai tủ có số sách bằng nhau. Số sách của tủ một là:

Điểm A thuộc nửa đường tròn (O;6cm) đường kính BC sao cho diện tích ΔABC lớn nhất. Khi đó số đo cung AC⌢là:

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho (O;R), AB là dây cung của đường (O) sao cho AB = $R \sqrt{3}$ . M là một điểm trên cung lớn AB. Số đo cung $\overset{⌢}{A M B}$ là bao nhiêu?

Giá trị nào của a thì đồ thị hàm số y = ax² đi qua điểm (−1; 2)?

Cặp số (x; y) nào sau đây là nghiệm của hệ phương trình ${\begin{cases} x + 3 y = 5 \\ 2 x - y = 3 \end{cases}$

Hàm số y = (m − 1)x² đồng biến với x < 0 khi:

Điểm A thuộc nửa đường tròn (O;6cm) đường kính BC sao cho diện tích ΔABC lớn nhất. Khi đó số đo cung $\overset{⌢}{A C}$ là: