Cho quang hệ gồm hai thấu kính O1 và O2 được đặt đồng trục chính. Thấu kính O2 có tiêu cự f2 = 9cm, vật sáng AB vuông góc với trục chính của quang hệ, trước thấu kính O1 và cách O1 một khoảng d1 = 12 cm (A thuộc trục chí nh của quang hệ). Thấu kính O2 ở sau O1. Sau thấu kính O2 đặt một màn ảnh E cố định vuông góc với trục chính của quang hệ, cách O1 một khoảng a = 60 cm. Giữ vật AB, thấu kính O1 và màn ảnh E cố định, dịch thấu kính O2 dọc theo trục chính của quang hệ trong khoảng giữa thấu kính O1 và màn người ta tìm được hai vị trí của thấu kính O2 để ảnh của vật cho bởi quang hệ hiện rõ nét trên màn E. Hai vị trí này cách nhau 24 cm.
1. Tính tiêu cự của thấu kính O1.
2. Tịnh tiến AB trước thấu kính O1, dọc theo trục chính của quang hệ. Tìm khoảng
cách giữa hai thấu kính để ảnh của vật cho bới quang hệ có độ cao không phụ thuộc vào vị trí của vật AB.
Cho quang hệ gồm hai thấu kính O1 và O2 được đặt đồng trục chính. Thấu kính O2 có tiêu cự f2 = 9cm, vật sáng AB vuông góc với trục chính của quang hệ, trước thấu kính O1 và cách O1 một khoảng d1 = 12 cm (A thuộc trục chí nh của quang hệ). Thấu kính O2 ở sau O1. Sau thấu kính O2 đặt một màn ảnh E cố định vuông góc với trục chính của quang hệ, cách O1 một khoảng a = 60 cm. Giữ vật AB, thấu kính O1 và màn ảnh E cố định, dịch thấu kính O2 dọc theo trục chính của quang hệ trong khoảng giữa thấu kính O1 và màn người ta tìm được hai vị trí của thấu kính O2 để ảnh của vật cho bởi quang hệ hiện rõ nét trên màn E. Hai vị trí này cách nhau 24 cm.
1. Tính tiêu cự của thấu kính O1.
2. Tịnh tiến AB trước thấu kính O1, dọc theo trục chính của quang hệ. Tìm khoảng
cách giữa hai thấu kính để ảnh của vật cho bới quang hệ có độ cao không phụ thuộc vào vị trí của vật AB.
Câu hỏi trong đề: Đề thi Vật lí ôn vào 10 hệ chuyên có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
1, Gọi ảnh của AB tạo bởi O1 cách O2 một khoảng d2 khi đó :
+ Khi di chuyển thấu kính lại gần màn 24 cm thì ảnh cách thấu kính O2 là :
+ Do khoảng cách giữa ảnh của AB tạo bởi O1 và màn không đổi nên.
d22 + 6d2 – 216 = 0
=> d2 = 12 (cm)
+ Do đó : = 36 (cm)
+ Khi đó ảnh của AB cách thấu kính O1 là :
d1’ = a – d2 – d2’ = 60 – 12 – 36 = 12 (cm)
+ vậy tiêu cự của thấu kính O1 là :
(cm)
2, Muốn ảnh AB tịnh tiến dọc theo trục chính đến bất kì vị trí nào trước thấu kính O1 để ảnh cuối cùng cho bởi quang hệ có chiều cao không phụ thuộc vào vị trí của vật thì hai thấu kính O1 và O2 có trục chính trùng nhau. Khi đó khoảng cách giữa hai thấu kính O1 và O2 là : O1O2 = f1 + f2 = 6 + 9 = 12 (cm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
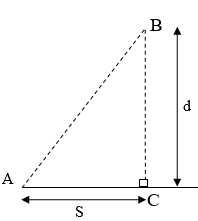
+ Gọi quãng đường DC có độ dài là: x
+ Độ dài quãng đường BD:
+ Thời gian người này đi từ A đến D rồi đến B là:
t = tAD + tDB =
+ Khi đó:
Khi đó =
v12v22t2 – 2Sv12v2t + s2v12 + v12d2 – v22d2 >= 0
v1v2d
+ Dẫn đến t ![]()
+ Đạt tại x =
+ Quãng đường mà người nay phải đi thỏa mãn yêu cầu bài toán là :
SAD + SDB = S – x +
Lời giải
+ Gọi nhiệt dung của bình 1, bình 2 và nhiệt kế lần lượt là q1, q2 và q.
+ Sau lần nhúng thứ ba vào bình 1 phương trình cân bằng nhiệt là :.
q1(80 – 78) = q(78 – 16) => q1 = 31q
+ Sau lần nhúng thứ tư vào bình 2 phương trình cân bằng nhiệt là :
q2(19 – 16) = q(78 – 19) => q2 = q
+ Sau lần nhúng thứ năm vào bình 1 phương trình cân bằng nhiệt là :
q1(78 – t) = q(t – 19) => 31q(78 – t) = q(t – 19) => t 76,20C
b, Sau một số lớn lần nhúng nhiệt kế ta coi như bài toán đổ hai chất lỏng vào nhau rồi thả nhiệt kế vào đó.
+ Khi đó phương trình cân bằng nhiệt là : q1(80 – t’) = (q2 + q)(t’ – 16)
=> 31q(80 – t’) = (t’ – 16)
=> t = 54,50C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.