Câu hỏi:

19/07/2022 1,264

Trong không gian Oxyz, cho mặt cầu (S) tâm I(9; 3; 1) bán kính bằng 3 . Gọi M, N là hai điểm lần lượt thuộc 2 trục Ox, Oz sao cho đường thẳng MN tiếp xúc với (S), đồng thời mặt cầu ngoại tiếp tứ diện OIMN có bán kính bằng $\frac{13}{2}$ . Gọi A là tiếp điểm của MN và (s), giá trị AM. AN bằng

A. 12 $\sqrt{3}$ .

B. 18.

C. 28 $\sqrt{3}$ .

D. 39.

Xem lời giải

Câu hỏi trong đề: Giải Đề thi THPT Quốc gia môn Toán năm 2022 (4 mã đề gốc) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: A

I(9; 3 ; 1) d = 3 = R Þ (S) tiếp xúc với (Oxz)

Gọi M( a; 0; 0) Î Ox $\Leftrightarrow$

N(0; 0; b) Î Oz

MN tiếp xúc với (S) tại A nên A là hình chiếu của I lên (Oxz)

Suy ra A(9; 0; 1)

Gọi K là trung điểm MN Þ K $(\frac{a}{2}; 0; \frac{b}{2})$

Gọi H là tâm mặt cầu ngoại tiếp tứ diện OIMN Þ OH = $\frac{13}{2}$ Þ HK MN

Gọi T là trung điểm OM Þ $\begin{matrix} O M ⊥ K T \\ O M ⊥ H T \end{matrix}\}$ Þ OM (KHT)

Þ OM HK Þ HK (OMN)

Mà IA (OMN) Þ HK// IA

Ta có : $\vec{A I}$ = (0; 3; 0)

$\vec{K H}$ = $(x_{H} - \frac{a}{2}; y_{H} - 0; z_{H} - \frac{b}{2})$

$\vec{A I}$ cùng phương $\vec{K H}$ nên $\{\begin{matrix} x_{H} = \frac{a}{2} \\ y_{H} = c (c \neq 0) \\ z_{H} = \frac{b}{2} \end{matrix}$

$\Rightarrow$ H $(\frac{a}{2}; c; \frac{b}{2})$

ỌH = $\frac{13}{2}$ $\Rightarrow$ $\frac{a^{2}}{2}$ + c² + $\frac{b^{2}}{4}$ = $\frac{169}{4}$ (1)

HI = OH = $\frac{13}{2}$ $\Rightarrow$ ${(\frac{a}{2} - 9)}^{2}$ + ${(c - 3)}^{2}$ + ${(\frac{b}{2} - 1)}^{2}$ = $\frac{169}{4}$ (2)

Từ (1) và (2) suy ra $\frac{a^{2}}{2}$ + c² + $\frac{b^{2}}{4}$ = ${(\frac{a}{2} - 9)}^{2}$ + ${(c - 3)}^{2}$ +

{(\frac{b}{2} - 1)}^{2}

$\Rightarrow$ 9a + b + 6c = 91 (3)

$\vec{A M}$ = (a − 9; 0; −1)

$\vec{A N}$ = (−9; 0; b − 1)

A, M, N thẳng hàng $\frac{a - 9}{- 9} = \frac{- 1}{b - 1}$

(a − 2)(b − 1) = 9

ab − a − 9b + 9 = 9

ab − a − 9b = 0

a(b − 1) = 9b

a = $\frac{9 b}{b - 1}$

Từ (3) $\Rightarrow$ 9. $\frac{9 b}{b - 1}$ + b + 6c = 91

$\frac{81 b}{b - 1}$ + b + 6c = 91

$\frac{b^{2} + 80 b}{b - 1}$ + 6c = 91 6c = 91 − $\frac{b^{2} + 80 b}{b - 1}$ = $\frac{- b^{2} + 11 b - 91}{b - 1}$

c = $\frac{- b^{2} + 11 b - 91}{6 (b - 1)}$

Ta có a² + 4c² + b² = 169

$\Leftrightarrow$ + 4 ${(\frac{- b^{2} + 11 b - 91}{6 (b - 1)})}^{2}$ + b² = 169

$\Leftrightarrow$ 9.81b² + (b⁴ + 121b² +8281− 22b³ + 182b² − 2002b) + 9b²(b − 1)² = 169 . 9 . (b − 1)²

$\Leftrightarrow$ 729b² + b⁴ +121b² +8281 − 22b³ + 182b² − 2002b + 9b⁴ − 18b³ +9b²= 1521b² − 3042b +1521

$\Leftrightarrow$ 10b⁴ − 40b³ − 480b² + 1040b +6760 = 0

$[\begin{matrix} b = 1 + 3 \sqrt{3} \Rightarrow a = \frac{9 (1 + 3 \sqrt{3})}{3 \sqrt{3}} = 9 + \sqrt{3} \\ b = 1 - 3 \sqrt{3} \Rightarrow a = = \frac{9 (1 - 3 \sqrt{3})}{- 3 \sqrt{3}} = 9 - \sqrt{3} \end{matrix}$

+ Trường hợp 1: a = 9 + $\sqrt{3}$ ; b = 1 + 3 Þ $\vec{A M}$ = $(\sqrt{3}; 0; - 1)$ Þ AM = 2

Þ $\vec{A N}$ = $(- 9; 0; 3 \sqrt{3})$ ÞAN = $\sqrt{108}$

AM.AN = 2. $\sqrt{108}$ = 12 $\sqrt{3}$

+ Trường hợp 2: a = 9 − $\sqrt{3}$ ; b = 1 − 3 $\sqrt{3}$ Þ $\vec{A M}$ = $(- \sqrt{3}; 0; - 1)$ Þ AM = 2

Þ $\vec{A N}$ = $(- 9; 0; - 3 \sqrt{3})$ Þ AN = $\sqrt{108}$

AM.AN = 2. $\sqrt{108}$ = 12 $\sqrt{3}$

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số f(x) = ax⁴ + bx² + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?

A. 1.

B. 6.

C. 7.

D. 5.

Lời giải

Đáp án đúng là: C

Dựa vào đồ thị ta thấy:

TH1. Phương trình f(x) = m có đúng hai nghiệm thực phân biệt khi m = −2:

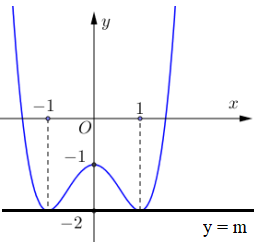
Media VietJack

TH2. Phương trình f(x) = m có đúng hai nghiệm thực phân biệt khi m > −1:

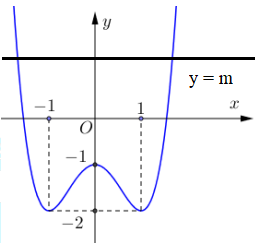
Media VietJack

Vậy m Î{−2; 0; 1; 2; 3; 4; 5}. Vậy có 7 giá trị m thỏa mãn.

Câu 2

Cho hình lập phương ABCD.A B C D có cạnh bằng 3 ( tham khảo hình bên). Khoảng cách từ B đến mặt phẳng (ACC A) bằng

A. $\frac{3 \sqrt{2}}{2}$

B. $\frac{3}{2}$

C. $3 \sqrt{2}$ .

D. 3

Lời giải

Đáp án đúng là: A

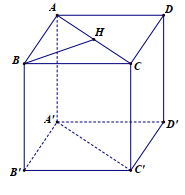
Gọi H là trung điểm của AC '

Vì ABCD.A'B'C'D'là hình lập phương nên BH (ACC'A')

Þ $(B, (A C C' A'))$ = BH = $\frac{1}{2}$ AC

Mà ABCD là hình vuông cạnh 3 nên AC =

Þ $(B, (A C C' A'))$ = $\frac{3 \sqrt{2}}{2}$

Câu 3

Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x − 2y + 2x + 3 = 0 là

A. (x + 1)² + (y + 2)² + (z + 3)² = 2.

B. (x − 1)² + (y − 2)² + (z − 3)² = 2.

C. (x + 1)² + (y + 2)² + (z + 3)² = 4.

D. (x − 1)² + (y − 2)² + (z − 3)² = 4.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho điểm M nằm ngoài mặt cầu S(O;R). Khẳng định nào dưới đây đúng ?

A. OM ≤ R.

B. OM > R.

C. OM = R.

D. OM < R.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Nếu $\int_{0}^{3} f (x) d x$ = 6 thì $\int_{0}^{3} [\frac{1}{3} f (x) + 2]$ dx bằng?

A. 8.

B. 5.

C. 9.

D. 6.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số y = f(x) có đạo hàm f '(x) = x + 1 với mọi x Î R. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (−1; +¥).

B. (1; +¥).

C. (−¥; −1).

D. (−¥; 1).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian Oxyz. Cho hai vectơ $\vec{u}$ = (1; −4; 0) và $\vec{v}$ = (−1; −2; 1). Vectơ $\vec{u}$ + 3 $\vec{v}$ có tọa độ là

A. (−2; −6; 3).

B. (−4; −8; 4).

C. (−2; −10; −3).

D. (−2; −10; 3).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hàm số f(x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?

Cho hình lập phương ABCD.A B C D có cạnh bằng 3 ( tham khảo hình bên). Khoảng cách từ B đến mặt phẳng (ACC A) bằng

Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x − 2y + 2x + 3 = 0 là

Cho điểm M nằm ngoài mặt cầu S(O;R). Khẳng định nào dưới đây đúng ?

Nếu ∫03f(x)dx = 6 thì ∫0313f(x)+2 dx bằng?

Cho hàm số y = f(x) có đạo hàm f '(x) = x + 1 với mọi x Î R. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Trong không gian Oxyz. Cho hai vectơ u→ = (1; −4; 0) và v→ = (−1; −2; 1). Vectơ u→ + 3v→ có tọa độ là

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số f(x) = ax⁴ + bx² + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?

Nếu $\int_{0}^{3} f (x) d x$ = 6 thì $\int_{0}^{3} [\frac{1}{3} f (x) + 2]$ dx bằng?

Trong không gian Oxyz. Cho hai vectơ $\vec{u}$ = (1; −4; 0) và $\vec{v}$ = (−1; −2; 1). Vectơ $\vec{u}$ + 3 $\vec{v}$ có tọa độ là