Quảng cáo
Trả lời:
Lời giải
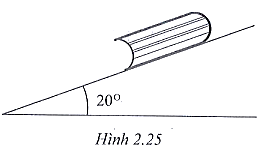
Thành phần pháp tuyến của lực tiếp xúc giữa sách và bề mặt mặt phẳng nghiêng là phản lực. Lực này cân bằng với thành phần theo phương vuông góc với mặt phẳng nghiêng của trọng lực:
\[N = {P_y} = mg\cos 20^\circ = 1,5.9,81.cos20^\circ = 13,83\left( N \right)\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Đáp án đúng là: A
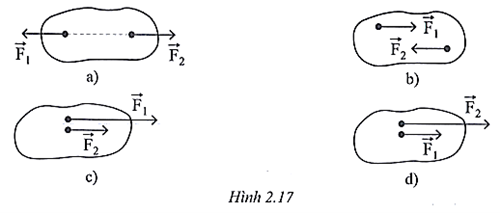
Lực \[\overrightarrow F \] sẽ gây tác dụng làm quay đối với vật khi giá của lực không đi qua trục quay.
Lời giải
Lời giải
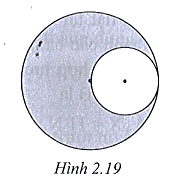
Trọng tâm của đĩa bị khoét là điểm đặt hợp lực của trọng lực PK của hình tròn tâm K bán kính \[\frac{R}{2}\] và trọng lực PI của phần đĩa còn lại sau khi khoét đi hai lỗ tròn đối xứng qua I.
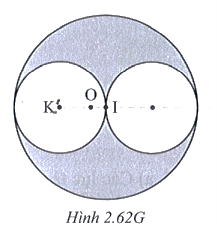
Ta có: \[IK = OK + OI = \frac{R}{2}\]
Vì đĩa phẳng đồng chất nên trọng lượng mỗi phần đĩa tỉ lệ với diện tích. Gọi P là trọng lượng của đĩa nguyên, ta có:
\[\frac{{{P_K}}}{P} = \frac{{\pi {{\left( {\frac{R}{2}} \right)}^2}}}{{\pi {R^2}}} = \frac{1}{4}\]\[ \Rightarrow {P_K} = \frac{P}{4};{P_I} = P - 2{P_K} = \frac{P}{2}\]
Áp dụng quy tắc hợp lực song song cùng chiều cho các trọng lực PI và PK, ta xác định được điểm đặt O của hợp lực sẽ chia đoạn thẳng IK theo tỉ lệ:
\[\frac{{OI}}{{OK}} = \frac{{{P_K}}}{{{P_I}}} = \frac{{\frac{P}{4}}}{{\frac{P}{2}}} = \frac{1}{2} \Rightarrow OI = \frac{R}{6}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.