Bài 1: Hình có trục đối xứng

Lời giải:

Trục đối xứng là đường thẳng mà khi gấp hình theo đường đó ta được hai phần chồng khít lên nhau.

Các đường nét đứt là trục đối xứng của mỗi hình.

Hình a) có một trục đối xứng được biểu diễn như hình sau:

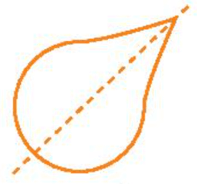
Hình b) có một trục đối xứng được biểu diễn như hình sau:

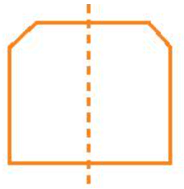
Hình c) có bốn trục đối xứng được biểu diễn như các hình sau:

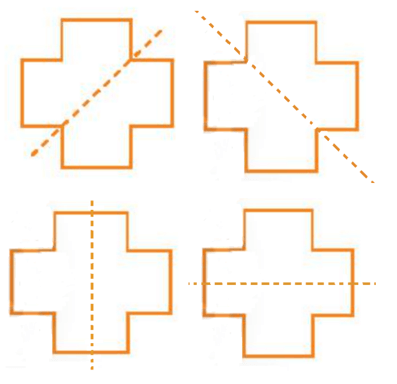
Lời giải:

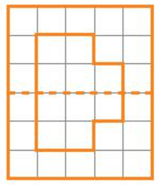
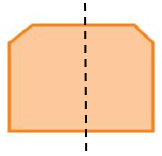
Hình a), b), d) có đường nét đứt chia hình đó thành hai phần bằng nhau nên những hình này có trục đối xứng.

Hình c) có đường nét đứt chia hình đó thành hai phần không bằng nhau nên hình này không có trục đối xứng.

Vậy hình a), b), d) có đường nét đứt là trục đối xứng.

Lời giải:

Trục đối xứng là số đường thẳng chia hình đó thành hai phần bằng nhau (giống hệt nhau).

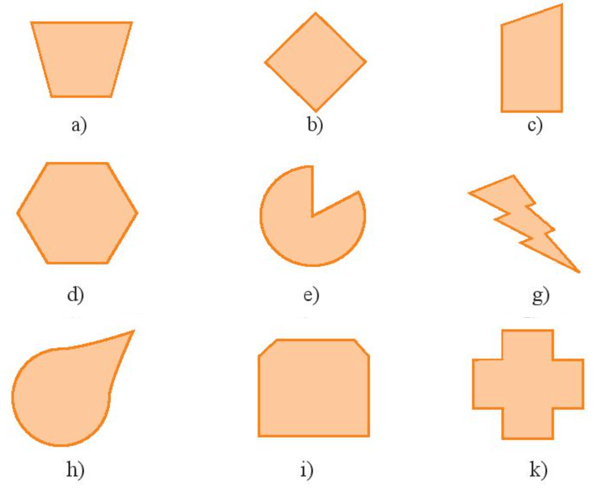
Số các trục đối xứng của các hình được biểu diễn như sau:

Hình a) có 1 trục đối xứng.

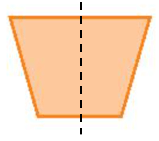
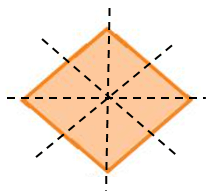
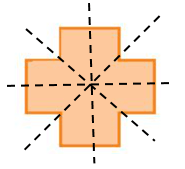
Hình b) có 4 trục đối xứng.

Hình c) không có trục đối xứng.

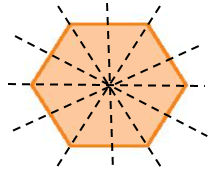
Hình d) có 6 trục đối xứng.

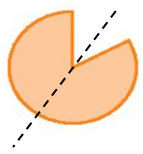
Hình e) có 1 trục đối xứng.

Hình g) không có trục đối xứng.

Hình h) có 1 trục đối xứng.

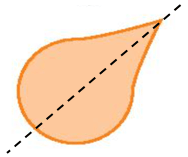
Hình i) có 1 trục đối xứng.

Hình k) có 4 trục đối xứng.

Vậy số các trục đối xứng trong mỗi hình như sau:

Lời giải:

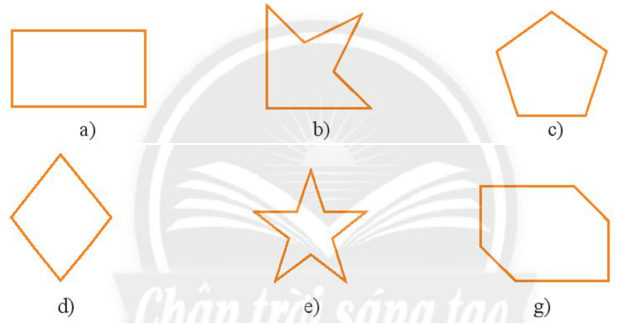
Một trục đối xứng của các hình được biểu diễn như sau:

Hình a) 

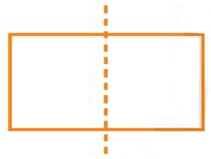
Hình b)

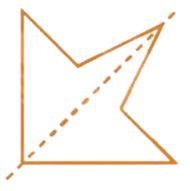
Hình c)

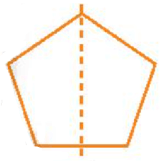
Hình d)

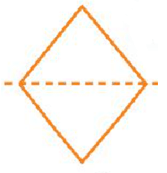
Hình e)

Hình g) không có trục đối xứng.

Lời giải:

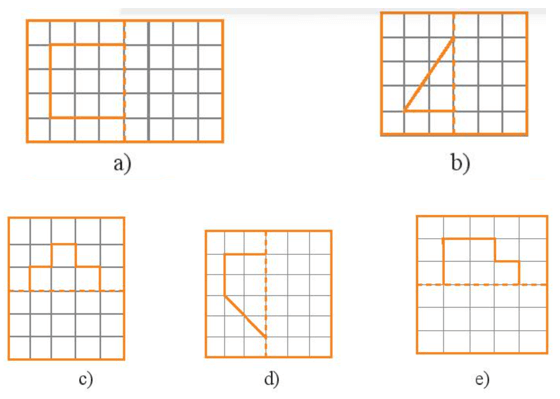
Coi đường nét đứt như một cái gương, vẽ thêm sao cho khi gập hình theo đường nét đứt ta được hai phần giống hệt và chồng khít lên nhau.

Hình sau khi được vẽ thêm có đường nét đứt là trục đối xứng được biểu diễn như sau:

Hình a)

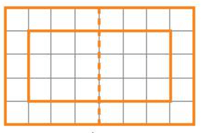
Hình b)

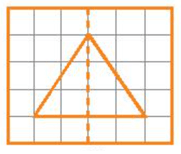
Hình c)

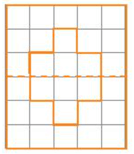
Hình d)

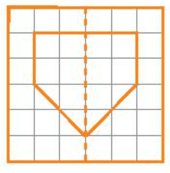
Hình e)