Câu hỏi:

13/07/2024 4,776

Cho biểu thức $P = (\frac{x - 1}{x^{2} - 2 x} + \frac{x + 1}{x^{2} + 2 x} - \frac{4}{x^{3} - 4 x}) : (1 - \frac{2}{x}) .$

a) Tìm điều kiện xác định và rút gọn biểu thức P.

b) Tính giá trị của biểu thức P biết x là số thực thỏa mãn điều kiện: |2x - 1| = 5.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Ta có:

$P = (\frac{x - 1}{x^{2} - 2 x} + \frac{x + 1}{x^{2} + 2 x} - \frac{4}{x^{3} - 4 x}) : (1 - \frac{2}{x})$

$= (\frac{x - 1}{x (x - 2)} + \frac{x + 1}{x (x + 2)} - \frac{4}{x (x - 2) (x + 2)}) : (1 - \frac{2}{x})$

ĐKXĐ:

$\{\begin{matrix} x - 2 \neq 0 \\ x + 2 \neq 0 \\ x \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 2 \\ x \neq - 2 \\ x \neq 0 \end{matrix}$

Suy ra:

$P = (\frac{x - 1}{x (x - 2)} + \frac{x + 1}{x (x + 2)} - \frac{4}{x (x - 2) (x + 2)}) : (1 - \frac{2}{x})$

$= (\frac{x - 1}{x (x - 2)} + \frac{x + 1}{x (x + 2)} - \frac{4}{x (x - 2) (x + 2)}) : (\frac{x - 2}{x})$

$= (\frac{x - 1}{x (x - 2)} + \frac{x + 1}{x (x + 2)} - \frac{4}{x (x - 2) (x + 2)}) . (\frac{x}{x - 2})$

$= \frac{x - 1}{{(x - 2)}^{2}} + \frac{x + 1}{(x - 2) (x + 2)} - \frac{4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{(x - 1) (x + 2)}{{(x - 2)}^{2} (x + 2)} + \frac{(x + 1) (x - 2)}{{(x - 2)}^{2} (x + 2)} - \frac{4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{x^{2} - x + 2 x - 2}{{(x - 2)}^{2} (x + 2)} + \frac{x^{2} + x - 2 x - 2}{{(x - 2)}^{2} (x + 2)} - \frac{4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{x^{2} - x + 2 x - 2 + x^{2} + x - 2 x - 2 - 4}{{(x - 2)}^{2} (x + 2)}$

$= \frac{2 x^{2} - 8}{{(x - 2)}^{2} (x + 2)} = \frac{2 (x^{2} - 4)}{{(x - 2)}^{2} (x + 2)}$

$= \frac{2 (x - 2) (x + 2)}{{(x - 2)}^{2} (x + 2)} = \frac{2}{x - 2}$

b) Xét phương trình |2x - 1| = 5 ⇔ $[\begin{matrix} 2 x - 1 = 5 \\ 2 x - 1 = - 5 \end{matrix} \Leftrightarrow [\begin{matrix} 2 x = 6 \\ 2 x = - 4 \end{matrix} \Leftrightarrow [\begin{matrix} x = 3 \\ x = - 2 \end{matrix}$

Đối chiếu ĐKXĐ ta suy ra được x = 3 là nghiệm của phương trình trên.

Thay x = 3 (TMĐK) vào biểu thức P, ta được:

$P = \frac{2}{3 - 2} = \frac{2}{1} = 2.$

Vậy với x thỏa mãn điều kiện |2x - 1| = 5 thì P = 2.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho x, y là hai số thực thỏa mãn điều kiện x² + 2y² + 2xy + 7x + 7y + 10 = 0. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức $P = \frac{2 x + 2 y - 3}{x + y + 6} .$

Xem đáp án

Lời giải

Ta có:

x² + 2y² + 2xy + 7x + 7y + 10 = 0

Û (x² + 2xy + y²) + 7x + 7y + y² + 10 = 0

Û (x + y)² + 7(x + y) + y² + 10 = 0 (1)

Đặt S = x + y nên suy ra phương trình (1) trở thành

(1) Û S² + 7S + y² + 10 = 0

$\Leftrightarrow S^{2} + 7 S + \frac{49}{4} = \frac{9}{4} - y^{2}$

$\Leftrightarrow {(S + \frac{7}{2})}^{2} = \frac{9}{4} - y^{2} \leq \frac{9}{4}$

Dấu “=” xảy ra Û $\frac{9}{4} - y^{2} = \frac{9}{4} \Leftrightarrow y = 0$

Vậy ${(S + \frac{7}{2})}^{2} \leq \frac{9}{4}$

\Leftrightarrow \frac{- 3}{2} \leq S + \frac{7}{2} \leq \frac{3}{2}

Û - 5 £ S £ -2

$P = \frac{2 x + 2 y - 3}{x + y + 6} = \frac{2 (x + y + 6) - 15}{x + y + 6}$

$= 2 - \frac{15}{x + y + 6} = 2 - \frac{15}{S + 6}$ (2)

Với - 5 £ S £ -2

Û 1 £ S + 6 £ 4

$\Leftrightarrow \frac{15}{4} \leq \frac{15}{S + 6} \leq 15$

$\Leftrightarrow 2 - 15 \leq 2 - \frac{15}{S + 6} \leq 2 - \frac{15}{4}$

$\Leftrightarrow - 13 \leq 2 - \frac{15}{S + 6} \leq - \frac{7}{4}$

$\Leftrightarrow - 13 \leq P \leq - \frac{7}{4}$

Vậy suy ra GTNN của P = -13 $\Leftrightarrow \{\begin{matrix} x = - 5 \\ y = 0 \end{matrix}$

Và GTLN của $P = \frac{- 7}{4} \Leftrightarrow \{\begin{matrix} x = - 2 \\ y = 0 \end{matrix} .$

Câu 2

Cho tam giác ABC vuông tại A (AB < AC) và các điểm D, E, F lần lượt là trung điểm của các cạnh BC, AB, AC. Lấy điểm M thuộc đoạn EB (M khác E và B). Kẻ đường thẳng qua D vuông góc với MD tại D, đường thẳng này cắt AC tại N.

a) Chứng minh tam giác DEM đồng dạng tam giác DFN.

b) Chứng minh tam giác DMN đồng dạng tam giác ACB.

c) Chứng minh MN² = BM² + CN².

Xem đáp án

Lời giải

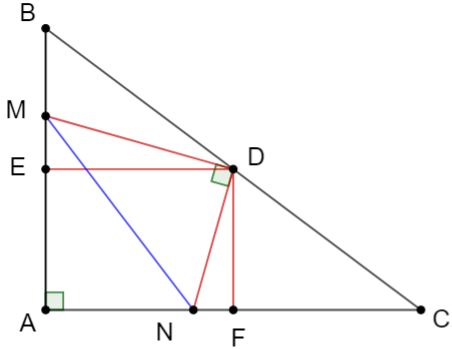
Media VietJack

a) +) Xét tam giác BAC có E, D lần lượt là trung điểm của BA và BC nên suy ra ED là đường trung bình của tam giác BAC

Þ ED // AC và $E D = \frac{A C}{2}; B E = \frac{A B}{2}$

Mà BA ^ AC nên suy ra BA ^ ED

Suy ra $\hat{M E D} = 90 °$

+) Xét tam giác CBA có F, D lần lượt là trung điểm của CA và CB nên suy ra FD là đường trung bình của tam giác BAC

Þ FD // AB và $F D = \frac{A B}{2}; C F = \frac{A C}{2}$

Mà BA ^ AC nên suy ra AC ^ FD

Suy ra $\hat{N F D} = 90 °$

+) Ta có:

ED // AC, FD // AB mà BA ^ AC nên suy ra ED ^ FD

$\Rightarrow \hat{E D N} + \hat{N D F} = 90 °$ (1)

Mà $\hat{M D N} = \hat{M D E} + \hat{E D N} = 90 °$ (2)

Từ (1) và (2) nên suy ra $\hat{M D E} = \hat{N D F}$ (Do cùng phụ với góc $\hat{E D N}$ )

Xét hai tam giác DDEM và DDFN có:

$\begin{matrix} \hat{M D E} = \hat{N D F} (c m t) \\ \hat{M E D} = \hat{N F D} (= 90 °) \end{matrix}\}$ ⇒ ∆DEM ᔕ DDFN (g – g)

b) Do DDEM ᔕ DDFN (g – g)

$\Rightarrow \frac{D M}{D N} = \frac{D E}{D F} = \frac{\frac{A C}{2}}{\frac{A B}{2}} = \frac{A C}{A B}$

$\Leftrightarrow \frac{D M}{A C} = \frac{D N}{A B}$

Xét hai tam giác DDMN và DACB có:

$\begin{matrix} \frac{D M}{A C} = \frac{D N}{A B} (c m t) \\ \hat{M D N} = \hat{C A B} (= 90 °) \end{matrix}\}$ ⇒ ∆DMN ᔕ DACB (c – g – c)

c) +) Ta có:

MN² = AM² + AN² = (AB - BM)² + (AC - CN)²

= AB² - 2AB.BM + BM² + AC² - 2AC.CN + CN²

= AB(AB - 2BM) + AC(AC - 2CN) + BM² + CN²

= AB(2BE - 2BM) + AC(2CF - 2CN) + BM² + CN²

= 2AB(BE - BM) - 2AC(CN - CF) + BM² + CN²

= 2AB.EM - 2AC.FN + BM² + CN² (3)

+) Lại có:

DDEM ᔕ DDFN (g.g)

$\Rightarrow \frac{E M}{F N} = \frac{D E}{D F} = \frac{\frac{A C}{2}}{\frac{A B}{2}} = \frac{A C}{A B}$

Û AB.EM = AC.FN (4)

Thay (4) vào (3) suy ra (3) trở thành

MN² = BM² + CN² (đpcm).

Câu 3

Một người lái ô tô dự định đi từ địa điểm A đến địa điểm B với vận tốc 48 km/h. Nhưng thực tế, sau khi đi được 1 giờ với vận tốc dự định, ô tô nghỉ trong 10 phút. Do đó để kịp đến B đúng thời gian dự định, người đó phải tăng vận tốc thêm 6 km/h trên quãng đường còn lại. Tính quãng đường AB.

b) Kích thước một bể bơi được cho trên hình vẽ (mặt nước có dạng hình chữ nhật). Hãy tính xem bể chứa được bao nhiêu mét khối nước khi nó đầy ắp nước (coi thành bể có độ dày không đáng kể; làm tròn kết quả đến hàng phần trăm).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải các phương trình và bất phương trình sau:

a) $\frac{2 x + 1}{2 x^{2} + 5 x + 2} - \frac{3}{x^{2} - 4} = 2;$

b) |x - 3| - |x² - x + 1| = 1;

c) (x² - 1)(x³ + 1) ³ 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho biểu thức P=x−1x2−2x+x+1x2+2x−4x3−4x:1−2x. a) Tìm điều kiện xác định và rút gọn biểu thức P. b) Tính giá trị của biểu thức P biết x là số thực thỏa mãn điều kiện: |2x - 1| = 5.

Cho x, y là hai số thực thỏa mãn điều kiện x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức P=2x+2y−3x+y+6.

Giải các phương trình và bất phương trình sau: a) 2x+12x2+5x+2−3x2−4=2; b) |x - 3| - |x2 - x + 1| = 1; c) (x2 - 1)(x3 + 1) ³ 0.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho x, y là hai số thực thỏa mãn điều kiện x² + 2y² + 2xy + 7x + 7y + 10 = 0. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức $P = \frac{2 x + 2 y - 3}{x + y + 6} .$

Giải các phương trình và bất phương trình sau:

a) $\frac{2 x + 1}{2 x^{2} + 5 x + 2} - \frac{3}{x^{2} - 4} = 2;$

b) |x - 3| - |x² - x + 1| = 1;

c) (x² - 1)(x³ + 1) ³ 0.