Cho tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh O, H, K. Biết \(\widehat A = \widehat O,\widehat B = \widehat K.\) Kí hiệu về sự bằng nhau của hai tam giác là:
Cho tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh O, H, K. Biết \(\widehat A = \widehat O,\widehat B = \widehat K.\) Kí hiệu về sự bằng nhau của hai tam giác là:
A. DABC = DKOH;
B. DABC = DHOK;
C. DABC = DOHK;
D. DABC = DOKH.
Quảng cáo
Trả lời:
Đáp án đúng là: D
Vì tam giác ABC và tam giác có ba đỉnh O, H, K bằng nhau, lại có \(\widehat A = \widehat O,\widehat B = \widehat K.\)
Do đó, nếu hai tam giác đó bằng nhau thì:
+ Đỉnh A của tam giác ABC tương ứng với đỉnh O của tam giác OHK;
+ Đỉnh B của tam giác ABC tương ứng với đỉnh K của tam giác OHK.
Khi đó đỉnh C của tam giác ABC tương ứng với đỉnh H của tam giác OHK.
Vậy kí hiệu bằng nhau của hai tam giác này là: DABC = DOKH.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\widehat {ABC} = \widehat {MNP};\)
B. \(\widehat {ABC} = \widehat {MPN};\)
C. AB = MP;
D. BC = MP.
Lời giải
Đáp án đúng là: A
Vì DABC = DMNP nên ta có:
+) \(\widehat {ABC} = \widehat {MNP}\) (hai góc tương ứng). Do đó A là đúng, B là sai.
+) AB = MN, BC = NP (các cặp cạnh tương ứng). Do đó C và D là sai.
Vậy ta chọn phương án A.
Câu 2
A. DABC = DMNP;
B. DABC = DMPN;
C. DABC = DNMP;
D. DABC = DNPM.
Lời giải
Đáp án đúng là: C
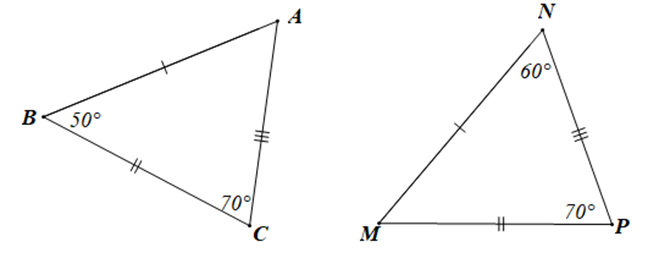
Xét tam giác ABC ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat A = 180^\circ - \widehat B - \widehat C\)
Hay \(\widehat A = 180^\circ - 50^\circ - 70^\circ = 60^\circ \)
Xét tam giác MNP ta có: \(\widehat M + \widehat N + \widehat P = 180^\circ \) (định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat M = 180^\circ - \widehat N - \widehat P\)
Hay \(\widehat M = 180^\circ - 60^\circ - 70^\circ = 50^\circ \)
Khi đó: tam giác ABC và tam giác MNP có:
+) AB = NM, BC = MP, AC = NP;
+) \(\widehat A = \widehat N\left( { = 60^\circ } \right),\widehat B = \widehat M\left( { = 50^\circ } \right),\widehat C = \widehat P\left( { = 70^\circ } \right)\)
Do đó hai tam giác ABC và MNP bằng nhau và được kí hiệu là DABC = DNMP.
Vậy ta chọn phương án C.
Câu 3
A. DABC = DMNP;
B. DABC = DPMN;
C. DABC = DMPN;
D. Cả B và C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. DABC = DDEG;
B. DABC = DDGE;
B. DABC = DDGE;
D. DABC = DEDG.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
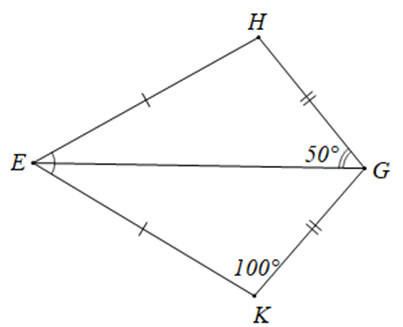
A. DEGH = DEKG;
B. DHEG = DKEG;
C. DEHG = DEGK;
D. DGEH = DGKE.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. DE;
B. DG;
C. EG;
D. Không có cạnh nào.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.