Xét bài toán “DOAB và DOAC có AB = AC, OB = OC (điểm O nằm ngoài tam giác ABC). Chứng minh rằng \(\widehat {OAB} = \widehat {OAC}\).”
Cho các câu sau:
(1) Suy ra DOAB = DOAC (c.c.c);
(2) AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
(3) Do đó \(\widehat {OAB} = \widehat {OAC}\) (hai góc tương ứng).
(4) Xét DOAB và DOAC có:
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
Xét bài toán “DOAB và DOAC có AB = AC, OB = OC (điểm O nằm ngoài tam giác ABC). Chứng minh rằng \(\widehat {OAB} = \widehat {OAC}\).”
Cho các câu sau:
(1) Suy ra DOAB = DOAC (c.c.c);
(2) AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
(3) Do đó \(\widehat {OAB} = \widehat {OAC}\) (hai góc tương ứng).
(4) Xét DOAB và DOAC có:
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
A. (2), (4), (1); (3);
B. (4), (2), (1), (3);
C. (1), (2), (3), (4);
D. (4), (2), (3), (1).
Quảng cáo
Trả lời:
Đáp án đúng là: B
Ta đi chứng minh \(\widehat {OAB} = \widehat {OAC}\) như sau:
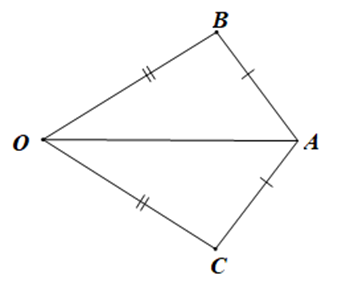
Xét DOAB và DOAC có:
AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
Suy ra DOAB = DOAC (c.c.c);
Do đó \(\widehat {OAB} = \widehat {OAC}\) (hai góc tương ứng).
Vậy ta chọn phương án B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
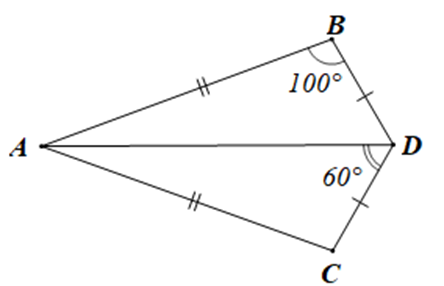
Câu 1
A. 20°;
B. 40°;
C. 80°;
D. 120°.
Lời giải
Đáp án đúng là: B
Xét tam giác ABD và tam giác ACD có:
AB = AC, BD = CD, AD là cạnh chung
Suy ra DABD = DACD (c.c.c)
Do đó \(\widehat {BAD} = \widehat {CAD},\widehat B = \widehat C,\widehat {BDA} = \widehat {CDA}\) (các cặp cạnh tương ứng)
Nên \(\widehat {BDA} = \widehat {CDA} = 60^\circ \)
Xét tam giác ABD có: \(\widehat {BAD} + \widehat B + \widehat {BDA} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \[\widehat {BAD} = 180^\circ - \widehat B - \widehat {BDA}\]
Hay \[\widehat {BAD} = 180^\circ - 100^\circ - 60^\circ = 20^\circ \]
Mà \(\widehat {BAD} = \widehat {CAD}\) nên \(\widehat {BAD} = \widehat {CAD} = 20^\circ \)
Mặt khác \(\widehat {BAC} = \widehat {BAD} + \widehat {CAD} = 20^\circ + 20^\circ = 40^\circ \)
Vậy số đo của \(\widehat {BAC}\) bằng 40°.
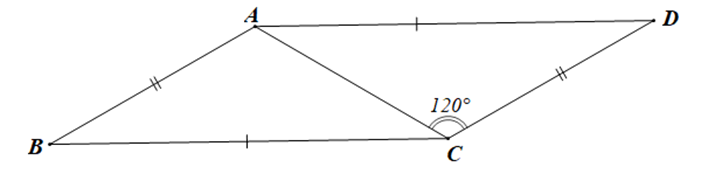
Câu 2
A. \(\widehat {BAC} = 30^\circ \) và AD không song song với BC;
B. \(\widehat {BAC} = 60^\circ \) và AD không song song với BC;
C. \(\widehat {BAC} = 60^\circ \) và AD // BC;
D. \(\widehat {BAC} = 120^\circ \) và AD // BC.
Lời giải
Đáp án đúng là: D
Xét tam giác ABC và tam giác ACD có:
AB = CD, BC = DA, AC là cạnh chung
Suy ra DABC = DCDA (c.c.c)
Do đó \(\widehat {BAC} = \widehat {DCA}\) (hai góc tương ứng)
Mà \(\widehat {DCA} = 120^\circ \)
Nên \(\widehat {BAC} = 120^\circ \)
Mặt khác: DABC = DCDA (chứng minh trên)
Suy ra \(\widehat {DAC} = \widehat {BCA}\) (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Do đó AD // BC (dấu hiệu nhận biết)
Vậy \(\widehat {BAC} = 120^\circ \) và AD // BC.
Câu 3
A. AD // CB;
B. AC // BD;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\widehat {AMD} = 90^\circ ;\)
B. AM // CN;
C. DABM = DAMD;
D. \(\widehat {BAM} = \widehat {ACN}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 20°;
B. 25°;
C. 40°;
D. 50°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
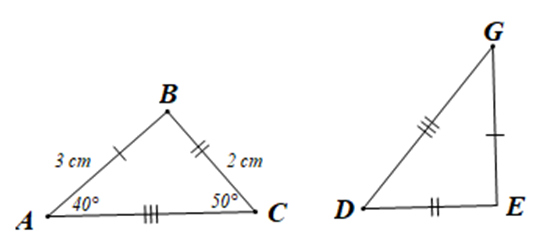
Câu 6
A. \(\widehat {DGE} = 40^\circ ,\) EG = 2 cm;
B. \(\widehat {DGE} = 50^\circ ,\) EG = 3 cm;
C. \(\widehat {DGE} = 40^\circ ,\) EG = 3 cm;
D. \(\widehat {DGE} = 50^\circ ,\) EG = 2 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.