Cho tứ giác ABCD, AB // DC, AB = DC, O là giao điểm của AC và BC. Khẳng định nào sau đây là đúng:
Cho tứ giác ABCD, AB // DC, AB = DC, O là giao điểm của AC và BC. Khẳng định nào sau đây là đúng:
A. AD // BC, AD = BC;
B. OA = OC, OB = OD;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Quảng cáo
Trả lời:
Đáp án đúng là: C
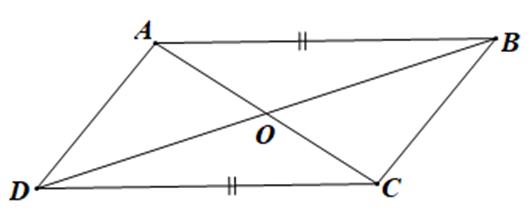
Vì AB // CD (giả thiết) nên \(\widehat {BAC} = \widehat {DCA}\) và \(\widehat {ABD} = \widehat {CDB}\) (các cặp góc so le trong)
Xét DOAB và DOCD có:
\[\widehat {BAO} = \widehat {DCO}\] (do \[\widehat {BAC} = \widehat {DCA}\]),
AB = CD (giả thiết),
\(\widehat {ABO} = \widehat {CDO}\) (do \(\widehat {ABD} = \widehat {CDB}\))
Do đó DOAB = DOCD (g.c.g)
Suy ra OA = OC và OB = OD (các cặp cạnh tương ứng)
Xét DAOD và DCOB có:
OA = OC (chứng minh trên),
\(\widehat {AOD} = \widehat {COB}\) (hai góc đối đỉnh),
OD = OB (chứng minh trên)
Do đó DAOD = DCOB (g.c.g)
Suy ra AD = CB (hai cạnh tương ứng)
Vậy ta chọn phương án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
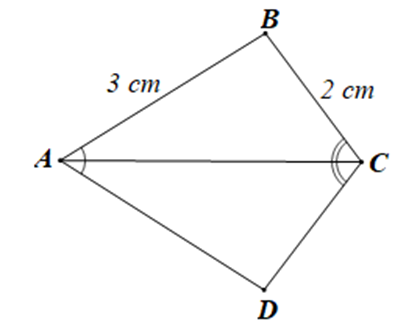
A. AB = DE;
B. AC = DF;
C. BC = EF;
D. \(\widehat {ACB} = \widehat {DFE}.\)
Lời giải
Đáp án đúng là: A
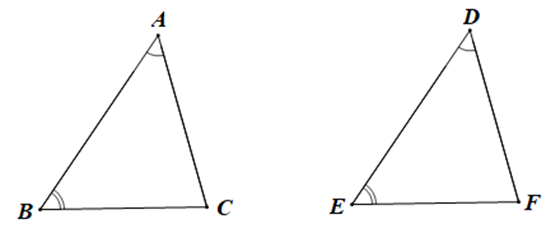
Để DABC = DDEF theo trường hợp góc – cạnh – góc mà \(\widehat A = \widehat D,\widehat B = \widehat E\) nên điều kiện còn thiếu là điều kiện về cạnh, sao cho hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh này, đó là AB = DE.
Vậy ta chọn phương án A.
Câu 2
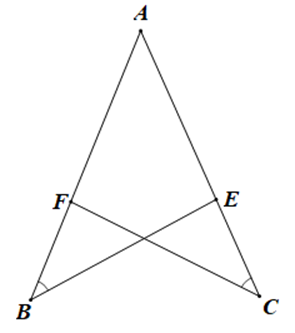
A. \(\widehat {AEB} = \widehat {AFC};\)
B. AB = AC;
C. BE = CF;
D. AF = AC.
Lời giải
Đáp án đúng là: B
Để ABE = DACF theo trường hợp góc – cạnh – góc với \(\widehat {ABE} = \widehat {ACF}\) và \(\widehat A\) chung thì cần thêm điều kiện về cạnh, sao cho hai cặp góc bằng nhau ở trên là hai góc kề của cặp cạnh đó.
Do đó điều điện cần thêm là AB = AC.
Vậy ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 25°;
B. 50°;
C. 100°;
D. Cả A, B, C đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\widehat {MHO} = \widehat {MGO};\)
B. MH = MG;
C. OH = OG;
D. Cả A, B, C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
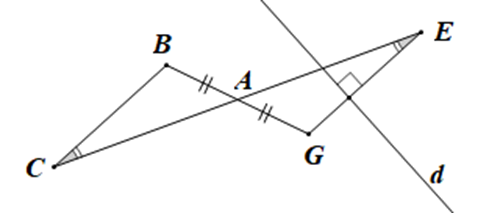
A. AB = AD ;
B. \(\widehat {ACB} = \widehat {AED};\)
C. AC = AE;
D. \(\widehat {BAC} = \widehat {DAE}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều đúng;
D. Cả (1) và (2) đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.