Công ty A thực hiện một cuộc khảo sát để tìm hiểu về mối liên hệ giữa y (sản phẩm) là số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y = ax + b (a, b là hằng số). Biết giá bán là 500 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 300 (sản phẩm); với giá bán 540 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 600 (sản phẩm).
a) Xác định a, b.
b) Bằng phép tính, hãy tính số lượng sản phẩm bán ra với giá bán là 480 000 đồng một sản phẩm?
Công ty A thực hiện một cuộc khảo sát để tìm hiểu về mối liên hệ giữa y (sản phẩm) là số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y = ax + b (a, b là hằng số). Biết giá bán là 500 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 300 (sản phẩm); với giá bán 540 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 600 (sản phẩm).
a) Xác định a, b.
b) Bằng phép tính, hãy tính số lượng sản phẩm bán ra với giá bán là 480 000 đồng một sản phẩm?
Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
Ta có: số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y = ax + b (a, b là hằng số).
Với giá bán là 500 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 300 (sản phẩm) thì ta có: 1 300 = a.500 000 + b.
Với giá bán 540 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 600 (sản phẩm) thì ta có: 1 600 = a.540 000 + b
Ta lập được hệ phương trình:
Û
b) Với a = 0,0075 và b = –2450 ta có:
y = 0,0075x – 2450.
Số sản phẩm bán được với giá bán là 480 000 đồng là:
y = 0,0075.480 000 – 2450 = 1 150 (sản phẩm)
Vậy với giá 480 000 đồng một sản phẩm thì bán ra được 1 150 sản phẩm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số học sinh làm bài 2 tờ giấy thi là x (x ∈ ℕ*) (học sinh)
Số học sinh làm bài 3 tờ giấy thi là y (y ∈ ℕ*) (học sinh)
Vì có 24 thí sinh dự thi mà có 3 thí sinh làm 1 tờ giấy thi nên ta có phương trình:
x + y + 3 = 24
Û x + y = 21 (1)
Vì tổng số tờ giấy thi là 59 tờ và có 3 thí sinh làm 1 tờ giấy thi nên ta có phương trình:
2x + 3y + 3 = 59
Û 2x + 3y = 56 (2)
Từ (1) và (2), ta có hệ phương trình:
Û
Û
Û (thỏa mãn)
Vậy có 7 thí sinh làm bài 2 tờ giấy thi và có 14 thí sinh làm 3 tờ giấy thi.
Lời giải
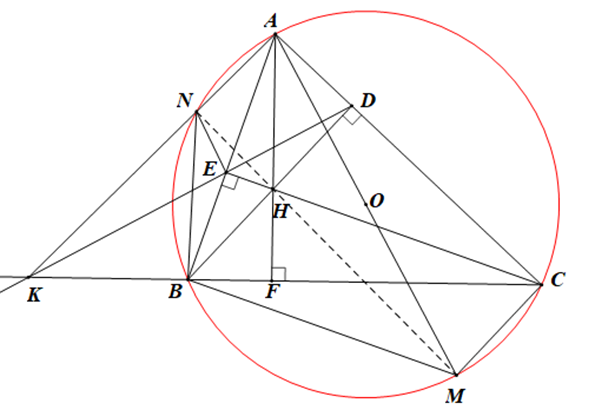
a) Ta có: = 90° (CE ^ AB), = 90° (BD ^ AC)
Þ = 90°
Mà và là hai góc có đỉnh kề nhau cùng nhìn cạnh BC của tứ giác BEDC.
Þ Tứ giác BEDC nội tiếp.
b) Ta có điểm C nằm trên đường tròn (O) đường kính AM
Nên = 90° (góc nội tiếp chắn nửa đường tròn)
Mà AH cắt BC tại F nên AF ⊥ BC do đó
Suy ra = 90°
Xét ∆ACM và ∆ABF, có:
= 90° (chứng minh trên),
(hai góc nội tiếp cùng chắn cung AC của (O))
Þ ∆ACM ᔕ ∆AFB (g.g)
Þ (tỉ số đồng dạng)
Þ AB.AC = AF.AM (đpcm).
c) • Tứ giác BEDC là tứ giác nội tiếp (chứng minh câu a)
Þ (hai góc nội tiếp cùng chắn cung EB)
Hay
Xét DKDB và DKCE có:
(Chứng minh trên),
là góc chung
Þ DKDB ᔕ DKCE (g.g)
(tỉ số đồng dạng)
Þ KB.KC = KD.KE (1)
• Tứ giác ANBC nội tiếp
Xét DKBN và DKAC có:
là góc chung,
(chứng minh trên)
Þ DKBN ᔕ DKAC (g.g)
(tỉ số đồng dạng)
Þ KB. KC = KA.KN (2)
Từ (1) và (2) ta có:
KD.KE = KA.KN (= KB. KC)
Xét DKNE và DKAD có:
là góc chung,
(chứng minh trên)
Þ DKNE ᔕ DKAD (c.g.c)
(hai góc tương ứng)
Þ Tứ giác ANED nội tiếp đường tròn.
Do đó 4 điểm A, N, E, D cùng thuộc một đường tròn (3)
• Tứ giác AEHD có
Þ E và D cùng thuộc đường tròn đường kính AH
Þ 4 điểm A, E, H, D cùng thuộc đường tròn đường kính AH (4)
Từ (3) và (4) suy ra 5 điểm A, N, E, H, D cùng thuộc đường tròn đường kính AH
Do đó tứ giác ANHD nội tiếp đường tròn
(góc nội tiếp chắn nửa đường tròn)
Þ AN ⊥ HN tại N (5)
• Ta có điểm N nằm trên đường tròn đường kính AM
= 90° (góc nội tiếp chắn nửa đường tròn)
Þ AN ⊥ MN tại N (6)
Từ (5) và (6) ta có: MN ≡ HN
Do đó ba điểm N, H, M thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.