Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 5)

Thi Online Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 5)

6994 lượt thi
6 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Cho phương trình: 3x² + 5x – 6 = 0 (x là ẩn)

a) Chứng minh phương trình có 2 nghiệm phân biệt. Tính tổng và tích 2 nghiệm của phương trình.

b) Không giải phương trình, hãy tính giá trị của biểu thức sau:

A = x₁² + x₁ + x₂ + x₂² −

Xem đáp án

a) 3x² + 5x – 6 = 0 (a = 3, b = 5, c = −6)

∆ = b² – 4ac = 5² – 4.3.(−6) = 97 > 0

Vì ∆ > 0 nên phương trình trên có hai nghiệm phân biệt.

Theo hệ thức Vi – ét ta có:

• S = x₁ + x₂ = $\frac{- b}{a}$ = $- \frac{5}{3}$

• P = x₁x₂ = $\frac{c}{a}$ = $- \frac{6}{3}$ = −2

b) A = x₁² + x₁ + x₂ + x₂² − $\frac{1}{9}$

= (x₁² + 2x₁x₂ + x₂²) – 2x₁x₂ + x₁ + x₂ − $\frac{1}{9}$

= (x₁ + x₂)² – 2x₁x₂ + (x₁ + x₂) − $\frac{1}{9}$

= ${(- \frac{5}{3})}^{2}$ − 2.(−2) + ${(- \frac{5}{3})}^{}$ − $\frac{1}{9}$

= $\frac{25}{9}$ + 4 – $\frac{5}{3}$ − $\frac{1}{9}$ = 5.

Vậy A = 5.

Câu 2:

Cho hàm số y = $- \frac{1}{2}$ x² có đồ thị (P) và hàm số y = x – 4 có đồ thị (D).

a) Vẽ (P) và (D) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán.

Xem đáp án

• Vẽ (P): y = x²

Bảng giá trị

x	−2	−1	0	1	2
y = $- \frac{1}{2} x^{2}$	−2	−	0	−	−2

Do đó (P) là đồ thị đi qua các điểm:

A(−2; –2); $B (- 1; - \frac{1}{2})$ ; O(0; 0); $C (1; - \frac{1}{2})$ ; D(2; –2).

•Vẽ (D): y = x – 4

Đường thẳng (D): y = x – 4 có a = 1, b = −4 đi qua 2 điểm M(0; b) và N $(\frac{- b}{a}; 0)$

Do đó 2 điểm thuộc đường thẳng (D) là M(0;−4) và N(4;0).

Ta vẽ được (P) và (D) như hình vẽ sau:

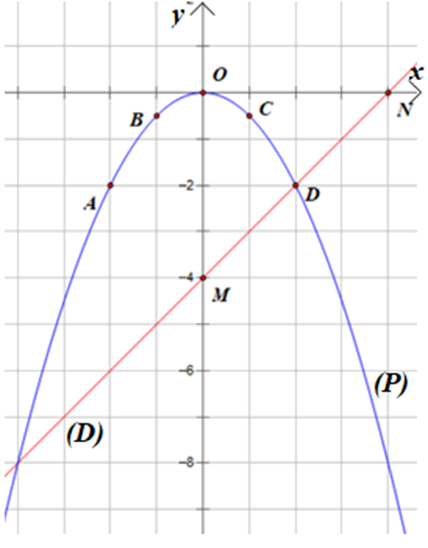
Cho hàm số y = x2 có đồ thị (P) và hàm số y = x – 4 có đồ thị (D). a) Vẽ (P) và (D) trên cùng hệ trục tọa độ. b) Tìm tọa độ giao điểm của (P) và (D) bằng phép toán. (ảnh 1)

b) Phương trình hoành độ giao điểm của (P) và (D) là:

$- \frac{1}{2}$ x² = x – 4

Û −x² = 2x – 8

Û −x² – 2x + 8 = 0

Û x² + 2x – 8 = 0

Û x² – 2x + 4x – 8 = 0

Û x(x – 2) + 4(x – 2) = 0

Û (x – 2)(x + 4) = 0

Û $[\begin{matrix} x - 2 = 0 \\ x + 4 = 0 \end{matrix}$ Û $[\begin{matrix} x = 2 \\ x = - 4 \end{matrix}$

• Thay x = 2 vào phương trình của (D): y = x – 4 ta được:

y = 2 – 4 = −2

Ta có tọa độ giao điểm (2; −2).

• Thay x = −4 vào phương trình của (D): y = x – 4 ta được:

y = −4 − 4 = −8

Ta có tọa độ giao điểm (−4; −8).

Vậy tọa độ giao điểm của (P) và (D) là (2; −2) và (−4; −8).

Câu 3:

Giải bài toán bằng cách lập hệ phương trình:

Trong kỳ thi học kì I môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát cho, cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 59 tờ giấy thi. Hỏi trong phòng thi có bao nhiêu thí sinh làm bài 2 tờ giấy thi, bao nhiêu thí sinh làm bài 3 tờ giấy thi? Biết rằng có 3 thí sinh chỉ làm 1 tờ giấy thi.

Xem đáp án

Gọi số học sinh làm bài 2 tờ giấy thi là x (x ∈ ℕ*) (học sinh)

Số học sinh làm bài 3 tờ giấy thi là y (y ∈ ℕ*) (học sinh)

Vì có 24 thí sinh dự thi mà có 3 thí sinh làm 1 tờ giấy thi nên ta có phương trình:

x + y + 3 = 24

Û x + y = 21 (1)

Vì tổng số tờ giấy thi là 59 tờ và có 3 thí sinh làm 1 tờ giấy thi nên ta có phương trình:

2x + 3y + 3 = 59

Û 2x + 3y = 56 (2)

Từ (1) và (2), ta có hệ phương trình:

$\{\begin{matrix} x + y = 21 \\ 2 x + 3 y = 56 \end{matrix}$

Û $\{\begin{matrix} 2 x + 2 y = 42 \\ 2 x + 3 y = 56 \end{matrix}$

Û $\{\begin{matrix} y = 14 \\ 2 x + 3.14 = 56 \end{matrix}$

Û $\{\begin{matrix} y = 14 \\ x = 7 \end{matrix}$ (thỏa mãn)

Vậy có 7 thí sinh làm bài 2 tờ giấy thi và có 14 thí sinh làm 3 tờ giấy thi.

Câu 4:

Công ty A thực hiện một cuộc khảo sát để tìm hiểu về mối liên hệ giữa y (sản phẩm) là số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y = ax + b (a, b là hằng số). Biết giá bán là 500 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 300 (sản phẩm); với giá bán 540 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 600 (sản phẩm).

a) Xác định a, b.

b) Bằng phép tính, hãy tính số lượng sản phẩm bán ra với giá bán là 480 000 đồng một sản phẩm?

Xem đáp án

Ta có: số lượng sản phẩm T bán ra với x (đồng) là giá bán ra của mỗi sản phẩm T và nhận thấy rằng y = ax + b (a, b là hằng số).

Với giá bán là 500 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 300 (sản phẩm) thì ta có: 1 300 = a.500 000 + b.

Với giá bán 540 000 đồng một sản phẩm thì số lượng sản phẩm bán ra là 1 600 (sản phẩm) thì ta có: 1 600 = a.540 000 + b

Ta lập được hệ phương trình:

$\{\begin{cases} 1 300 = a .500 000 + b \\ 1 600 = a .540 000 + b \end{cases}$

Û $\{\begin{matrix} 1 300 = a .500 000 + b \\ 40 000 a = 300 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 1 300 = 0, 0075.500 000 + b \\ a = 0, 0075 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} b = - 2450 \\ a = 0, 0075 \end{matrix}$

b) Với a = 0,0075 và b = –2450 ta có:

y = 0,0075x – 2450.

Số sản phẩm bán được với giá bán là 480 000 đồng là:

y = 0,0075.480 000 – 2450 = 1 150 (sản phẩm)

Vậy với giá 480 000 đồng một sản phẩm thì bán ra được 1 150 sản phẩm.

Câu 5:

Người ta thả một quả trứng vào cốc thủy tinh hình trụ có chứa nước, trứng chìm hoàn toàn xuống đáy cốc. Hỏi thể tích quả trứng dó là bao nhiêu cm³? (làm tròn đến hàng đơn vị). Biết cốc thủy hình trụ có đường kính đáy 10 cm và nước trong cốc dâng thêm 7,5 mm.

(Công thức tính thể tích hình trụ: V = pr²h, với r là bán kính đáy và h là chiều cao của hình trụ.)

Xem đáp án

Đổi 7,5 mm = 0,75 cm.

R = $\frac{d}{2}$ = $\frac{10}{2}$ = 5 cm.

Ta có thể tích của quả trứng chính là thể tích phần nước dâng lên.

Thể tích quả trứng là khoảng:

V = pr²h = p.5².0,75 ≈ 59 (cm³)

Vậy thể tích của quả trứng là khoảng 59 cm³.

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Đề kiểm tra 1 tiết Toán 9 Chương 3 Đại số có đáp án

( 4.4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 3 Đại số có đáp án

( 4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 4 Đại Số có đáp án

( 4.1 K lượt thi )

Đề kiểm tra 1 tiết Toán 9 Chương 4 Đại số có đáp án

( 2.9 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 3 Hình học có đáp án

( 4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 1 Đại Số (có đáp án)

( 8.5 K lượt thi )

Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án

( 7.4 K lượt thi )

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023

( 6.4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 1 Hình học có đáp án

( 6.1 K lượt thi )

Đề kiểm tra 1 tiết Toán 9 Chương 1 Đại Số có đáp án

( 5.4 K lượt thi )

Đánh giá trung bình

Thi Online Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án