Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 11)

Thi Online Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 11)

7006 lượt thi
5 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Không sử dụng máy tính cầm tay, hãy giải hệ phương trình và phương trình sau:

a) $\{\begin{matrix} 4 x - y = 5 \\ 3 x + y = 9 \end{matrix}$

b) x² + 4x – 5 = 0

Xem đáp án

a) $\{\begin{matrix} 4 x - y = 5 (1) \\ 3 x + y = 9 (2) \end{matrix}$

Cộng phương trình (1) và (2) vế theo vế ta được:

7x = 14 Û x = 2.

Thay x = 2 vào phương trình (1) ta được: 4.2 – y = 5 Û y = 3.

Vậy hệ phương trình có nghiệm là (2; 3).

b) x² + 4x – 5 = 0

Û x² – x + 5x – 5 = 0

Û x(x – 1) + 5(x – 1) = 0

Û (x + 5).(x – 1) = 0

Û $[\begin{matrix} x + 5 = 0 \\ x - 1 = 0 \end{matrix}$ Û $[\begin{matrix} x = - 5 \\ x = 1 \end{matrix}$ .

Vậy tập nghiệm của phương trình đã cho là S = {1; −5}.

Câu 2:

a) Vẽ đồ thị của hàm số y = 2x².

b) Gọi x₁, x₂ là hai nghiệm của phương trình bậc hai ẩn x:

x² – (3m + 1)x + 2m² + m – 1 = 0 (Với m là tham số).

Tìm giá trị của m sao cho: x₁² + x₂² – 3x₁x₂ = 4.

Xem đáp án

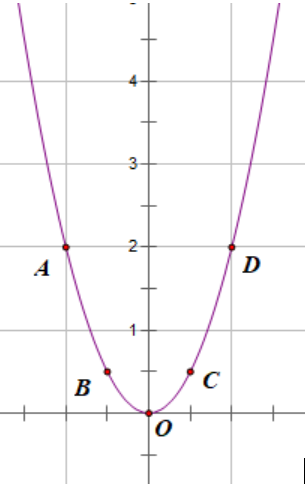
a) Bảng giá trị

x	−1	$- \frac{1}{2}$	0	$\frac{1}{2}$	1
y = 2x²	2	$\frac{1}{2}$	0	$\frac{1}{2}$	2

Trên mặt phẳng tọa độ lấy các điểm: A(−1; 2); B $(- \frac{1}{2}; \frac{1}{2})$ ; O(0; 0); C $(\frac{1}{2}; \frac{1}{2})$ ; D(1; 2).

a) Vẽ đồ thị của hàm số y = 2x2. b) Gọi x1, x2 là hai nghiệm của phương trình bậc hai ẩn x: x2 – (3m + 1)x + 2m2 + m – 1 = 0 (Với m là tham số). Tìm giá trị của m sao cho: x12 + x22 – 3x1x2 = 4. (ảnh 1)

b) x² – (3m + 1)x + 2m² + m – 1 = 0 (a = 1, b = −(3m + 1), c = 2m² + m – 1)

Ta có: ∆ = b² – 4ac = [−(3m + 1)]² – 4(2m² + m – 1)

= 9m² + 6m + 1 – 8m² – 4m + 4

= m² + 2m + 5

= m² + 2m + 1 + 4

= (m + 1)² + 4 > 0

Vì ∆ > 0 nên phương trình có hai nghiệm phân biệt với mọi m.

Theo định lý Vi-ét, ta có: $\{\begin{matrix} x_{1} + x_{2} = \frac{- b}{a} = 3 m + 1 \\ x_{1} x_{2} = \frac{c}{a} = 2 m^{2} + m - 1 \end{matrix}$

Theo đề bài, ta có: x₁² + x₂² – 3x₁x₂ = 4

Û (x₁ + x₂)² – 2x₁x₂ – 3x₁x₂ = 4

Û (3m + 1)² – 5(2m² + m – 1) = 4

Û 9m² + 6m + 1 – 10m² – 5m + 5 – 4 = 0

Û −m² + m + 2 = 0

Û m² – m – 2 = 0

Û m² – 2m + m – 2 = 0

Û (m – 2)(m + 1) = 0

Û $[\begin{matrix} m - 2 = 0 \\ m + 1 = 0 \end{matrix}$

Û $[\begin{matrix} m - 2 = 0 \\ m + 1 = 0 \end{matrix}$ .

Vậy giá trị của m thỏa mãn yêu cầu bài toán là: m = 2; m = −1.

Câu 3:

Giải bài toán sau bằng cách lập phương trình:

Tìm hai số tự nhiên, biết rằng hai số tự nhiên đó hơn kém nhau 3 đơn vị và tích của chúng bằng 108.

Xem đáp án

Gọi số tự nhiên thứ nhất cần tìm là x (x > 0).

Số tự nhiên thứ hai cần tìm là x – 3.

Theo đề bài, tích của hai số tự nhiên bằng 108 nên ta có phương trình:

x(x – 3) = 108

Û x² – 3x – 108 = 0

Û x² + 9x – 12x – 108 = 0

Û x(x + 9) – 12(x + 9) = 0

Û (x + 9)(x – 12) = 0

Û $[\begin{matrix} x + 9 = 0 \\ x - 12 = 0 \end{matrix}$

Û $[\begin{matrix} x = - 9 (K T M) \\ x = 12 (T M) \end{matrix}$

Vậy số tự nhiên thứ nhất cần tìm là 12 và số tự nhiên thứ hai cần tìm là 12 – 3 = 9.

Câu 4:

a) Tính diện tích của một mặt cầu, biết bán kính của mặt cầu đó bằng 6 cm.

b) Biết một hình nón có bán kính đường tròn đáy là 8 cm và độ dài đường sinh là 17 cm. Tính thể tích của hình nón đó.

Xem đáp án

a) Ta có công thức tính diện tích mặt cầu là S = 4p.R³

Thay R = 6cm vào S, ta được:

4p.6³ = 864p (cm²).

Vậy diện tích của một mặt cầu cần tìm là 864p cm².

b) Ta có R_đáy = = 4 cm.

Chiều cao hình nón là:

h = $\sqrt{l^{2} - r^{2}}$ = $\sqrt{l^{2} - r^{2}}$ = $\sqrt{l^{2} - r^{2}}$ (cm)

Thể tích hình nón là:

V = $\frac{1}{3}$ pR².h = $\frac{1}{3}$ p.4². $\sqrt{273}$ ≈ 276,8 (cm³).

Vậy thể tích của hình nón khoảng 276,8 cm³.

Câu 5:

Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O. Kẻ đường cao AH. Từ điểm H kẻ HM vuông góc với AB (M Î AB) và HN vuông góc với AC (N Î AC).

a) Chứng minh: Tứ giác AMHN nội tiếp.

b) Chứng minh: $\hat{A M N} = \hat{A C B}$

c) Tia MN cắt đường tròn (O) tại điểm D. Chứng minh: AD² = AN.AC.

Xem đáp án

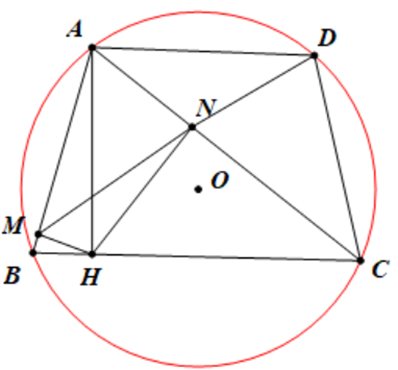
Cho tam giác ABC có ba góc nhọn, nội tiếp đường tròn tâm O. Kẻ đường cao AH. Từ điểm H kẻ HM vuông góc với AB (M  AB) và HN vuông góc với AC . (ảnh 1)

a) Ta có: HM ^ AB Þ $\hat{H M B} = \hat{H M A} = 90 °$

HN ^ AC Þ $\hat{H N A} = \hat{H N C} = 90 °$

Xét tứ giác AMHN có $\hat{H M A} + \hat{H N A}$ = 90° + 90° = 180°.

Mà hai góc nằm ở vị trí đối nhau.

Do đó tứ giác AMHN nội tiếp.

b) Ta có $\hat{A M N} = \hat{A H N}$ (chứng minh trên)

Suy ra $\hat{A H N} + \hat{N H C}$ = $\hat{A H C}$ = 90°

Mà $\hat{N H C} + \hat{N C H}$ = 90° (∆HNC có $\hat{H N C}$ = 90°)

Nên $\hat{A H N} = \hat{N C H}$ hay $\hat{A H N} = \hat{A C B}$

Mà $\hat{A M N} = \hat{A H N}$

Do đó $\hat{A C B} = \hat{A M N}$ .

c) Ta có $\hat{A M N} + \hat{B M N} = 180 °$

Suy ra $\hat{A C B} + \hat{B M N}$ = 180° hay $\hat{B M N} + \hat{B C N}$ = 180°

Do đó tứ giác BMNC nội tiếp.

Suy ra $\hat{M B C} + \hat{M N C}$ = 180° hay $\hat{A B C} + \hat{M N C}$ = 180°

Mà tứ giác ADCB nội tiếp đường tròn (O) nên $\hat{A B C} + \hat{A D C}$ = 180°.

Suy ra $\hat{M N C} = \hat{A D C}$ mà $\hat{A N D} = \hat{M N C}$ (hai góc đối đỉnh)

Do đó $\hat{A N D} = \hat{A D C}$

Xét ∆AND và ∆ADC có:

$\hat{C A D}$ chung

$\hat{A N D} = \hat{A D C}$ (cmt)

Do đó ∆AND ∆ADC (g.g)

Suy ra $\frac{A N}{A D} = \frac{A D}{A C}$

Do đó AD² = AN.AC (đpcm).

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan: