Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 6)

Thi Online Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 6)

6990 lượt thi
7 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

(1,5 điểm) Giải các phương trình

a) 2x² – 5x + 2 = 0;

b) x⁴ + x² – 6 = 0.

Xem đáp án

a) 2x² – 5x + 2 = 0

Cách 1:

Ta có D = (–5)² – 4.2.2 = 9 > 0

Khi đó phương trình đã cho có hai nghiệm phân biệt

$x_{1} = \frac{5 + \sqrt{9}}{2.2} = 2$ và $x_{2} = \frac{5 - \sqrt{9}}{2.2} = \frac{1}{2}$

Vậy phương trình đã cho có tập nghiệp $S = \{2; \frac{1}{2}\}$

Cách 2:

2x² – 5x + 2 = 0

Û x² − $\frac{5}{2}$ x + 1 = 0

Û x² − $\frac{1}{2}$ x – 2x + 1 = 0

Û x $(x - \frac{1}{2})$ − 2 $(x - \frac{1}{2})$ = 0

Û (x – 2) $(x - \frac{1}{2})$ = 0

Û $[\begin{matrix} x - 2 = 0 \\ x - \frac{1}{2} = 0 \end{matrix}$ Û $[\begin{matrix} x = 2 \\ x = \frac{1}{2} \end{matrix}$ .

Vậy phương trình đã cho có tập nghiệp $S = \{2; \frac{1}{2}\}$

b) x⁴ + x² – 6 = 0 (1)

Đặt t = x² (t ≥ 0), phương trình (1) trở thành:

t² + t – 6 = 0 (2)

Ta có hai cách giải phương trình (2) như sau:

Cách 1:

Ta có D = 1² – 4.1.(–6) = 25 > 0

Khi đó phương trình đã cho có hai nghiệm phân biệt là:

$t_{1} = \frac{- 1 + \sqrt{25}}{2.1} = 2$ (thỏa mãn) và $t_{2} = \frac{- 1 - \sqrt{25}}{2.1} = - 3$ (không thỏa mãn)

Cách 2:

t² + t – 6 = 0 (2)

Û t² – 2t + 3t – 6 = 0

Û t(t – 2) + 3(t – 2) = 0

Û (t – 2)(t + 3) = 0

Û $[\begin{matrix} t - 2 = 0 \\ t + 3 = 0 \end{matrix}$

Û t = 2 (thỏa mãn) hay t = −3 (không thỏa mãn).

Với t = 2, ta có: x² = 2

Û x = $\sqrt{2}$ hoặc x = $- \sqrt{2}$ .

Vậy phương trình đã cho có tập nghiệm $S = \{\sqrt{2}; - \sqrt{2}\} .$

Câu 2:

(1,5 điểm)

a) Vẽ đồ thị (P) của hàm số y = $\frac{x^{2}}{2}$ và đồ thị (D) của hàm số y = −3x – 4 trên cùng hệ trục tọa độ.

b) Tính tọa độ các giao điểm của đồ thị (P) và đồ thị (D).

Xem đáp án

+ Vẽ (P): y = $\frac{x^{2}}{2}$

Bảng giá trị

x	−2	−1	0	1	2
y = $\frac{x^{2}}{2}$	2	$\frac{1}{2}$	0	$\frac{1}{2}$	2

Do đó (P) là đồ thị đi qua các điểm:

A(−2; 2); $B (- 1; \frac{1}{2})$ ; O(0; 0); $C (1; \frac{1}{2})$ ; D(2; 2).

+ Vẽ (D): y = −3x – 4

Đường thẳng (D): y = −3x – 4 có a = −3, b = −4 đi qua 2 điểm M(0; b) và N $(\frac{- b}{a}; 0)$

Do đó 2 điểm thuộc đường thẳng (D) là M(0;−4) và N $(\frac{- 4}{3}; 0)$

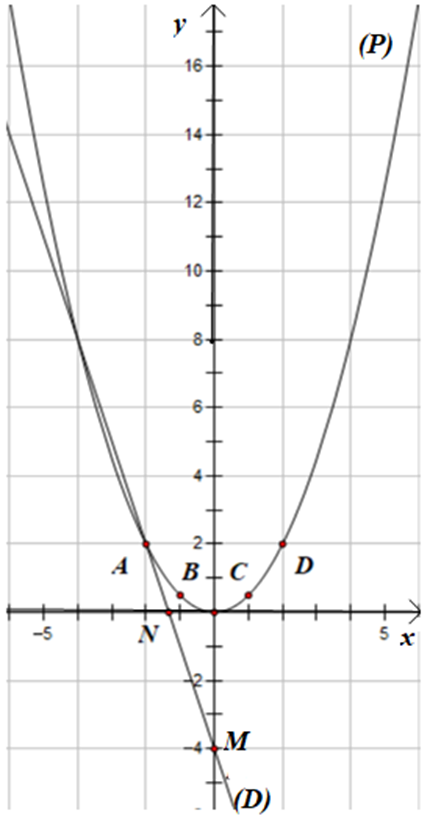
a) Vẽ đồ thị (P) của hàm số y = và đồ thị (D) của hàm số y = −3x – 4 trên cùng hệ trục tọa độ. b) Tính tọa độ các giao điểm của đồ thị (P) và đồ thị (D). (ảnh 1)

b) Phương trình hoành độ giao điểm của (P) và (D) là:

$\frac{1}{2}$ x² = −3x – 4

Û x² = –6x – 8

Û x² + 6x + 8 = 0

Û x² + 4x + 2x + 8 = 0

Û x(x + 4) + 2(x + 4) = 0

Û (x + 4)(x + 2) = 0

Û $[\begin{matrix} x + 4 = 0 \\ x + 2 = 0 \end{matrix}$

Û $[\begin{matrix} x = - 2 \\ x = - 4 \end{matrix}$

• Thay x = −2 vào phương trình của (D): y = −3x – 4 ta được:

y = −3.(−2) − 4 = 2

Ta có tọa độ giao điểm là (−2; 2).

• Thay x = −4 vào phương trình của (D): y = −3x – 4 ta được:

y = −3.(−4) − 4 = 8

Ta có tọa độ giao điểm là (−4; 8).

Vậy tọa độ các giao điểm của (P) và (D) là (−2; 2) và (−4; 8).

Câu 3:

(1,5 điểm) Cho phương trình: x² + 2mx + m² + 2m – 2 = 0 (1) (x là ẩn).

a) Tìm giá trị của m để phương trình (1) có hai nghiệm.

b) Gọi x₁, x₂ là hai nghiệm của phương trình (1). Tìm giá trị của m để x₁x₂ + x₁ + x₂ = 0.

Xem đáp án

x² + 2mx + m² + 2m – 2 = 0 có a = 1, b = 2m, c = m² + 2m – 2

Ta có:

∆ = b² – 4ac

= (2m)² – 4.1.(m² + 2m – 2)

= -8m + 8

a) Để phương trình (1) có hai nghiệm Û ∆ ≥ 0

Û −8m + 8 ≥ 0 Û m ≤ 1.

Vậy với m ≤ 1 thì phương trình (1) có hai nghiệm.

b) Với m ≤ 1, phương trình (1) có hai nghiệm x₁, x₂

Theo hệ thức Vi – ét ta có:

$\{\begin{matrix} x_{1} + x_{2} = \frac{- b}{a} = - 2 m \\ x_{1} x_{2} = \frac{c}{a} = m^{2} + 2 m - 2 \end{matrix}$

Ta có: x₁x₂ + x₁ + x₂ = 0

Û m² + 2m – 2 – 2m = 0

Û m² = 2

Û m = $\sqrt{2}$ (không thỏa mãn) hoặc m = $- \sqrt{2}$ (thỏa mãn)

Vậy m = $- \sqrt{2}$ thỏa mãn yêu cầu bài toán.

Câu 4:

(1,0 điểm) Lớp 9A có 42 học sinh. Vừa qua lớp đã phát động phong trào tặng sách cho các bạn khó khăn ở vùng sâu. Tại buổi phát động, mỗi học sinh trong lớp đều tặng 3 quyển sách hoặc 5 quyển sách. Kết quả cả lớp đã tặng được 146 quyển sách. Hỏi lớp 9A có bao nhiêu bạn tặng 3 quyển sách và bao nhiêu bạn tặng 5 quyển sách?

Xem đáp án

Gọi số học sinh tặng 3 quyển sách của lớp 9A là x (x ∈ ℕ*) (bạn).

Số học sinh tặng 5 quyển sách của lớp 9A là y (y ∈ ℕ*) (bạn).

Vì lớp 9A có 42 học sinh nên ta có phương trình: x + y = 42 (1)

Vì cả lớp 9A đã tặng được 146 quyển sách nên ta có phương trình:

3x + 5y = 146 (2)

Từ (1) và (2), ta có hệ phương trình:

Û $\{\begin{matrix} x + y = 42 \\ 3 x + 5 y = 146 \end{matrix}$

$\{\begin{matrix} 3 x + 3 y = 126 (3) \\ 3 x + 5 y = 146 (4) \end{matrix}$

Ta lấy phương trình (4) trừ phương trình (3) vế theo vế ta được phương trình:

2y = 20

Û y = 10 (thỏa mãn)

Thay y = 10 vào phương trình (1) ta được:

x + 10 = 42 Û x = 32 (thỏa mãn)

Vậy lớp 9A có 32 bạn tặng 3 quyển sách và 10 bạn tặng 5 quyển sách.

Câu 5:

(1,0 điểm) Một cửa hàng bán loại kem lạnh A như sau: nếu mua không quá 3 hộp thì giá 40 nghìn đồng mỗi hộp, nếu mua nhiều hơn 3 hộp thì bắt đầu từ hộp thứ tư trở đi giá mỗi hộp sẽ giảm đi 20% so với giá ban đầu.

a) Viết công thức tính y (số tiền mua kem) theo x (số hộp kem mua được trong trường hợp mua nhiều hơn 3 hộp).

b) An và Bình đều mua loại kem lạnh A với số hộp nhiều hơn 3. Biết rằng số hộp kem An mua gấp đôi số hộp Bình mua, đồng thời tổng số tiền mua kem của hai bạn là 624 nghìn đồng, hỏi bạn Bình mua bao nhiêu hộp kem? Giải thích.

Xem đáp án

a) Gọi y là số tiền mua kem (nghìn đồng) (y > 0).

x là số hộp kem mua được (hộp) (x > 3, x ∈ ℕ*).

Số tiền khi mua 3 hộp kem là:

3.40 = 120 (nghìn đồng)

Số hộp kem được tính với giá 20% là:

x – 3 (hộp kem)

Giá mỗi hộp kem (từ hộp thứ tư trở đi) là:

(100% – 20%).40 = 32 (nghìn đồng)

Số tiền cần trả khi mua nhiều hơn 3 hộp kem là:

y = 120 + (x – 3).32

= 32x + 24 (nghìn đồng).

b) Gọi a (hộp) là số hộp kem Bình mua (a > 3, a ∈ ℕ*)

Khi đó số hộp kem An mua là 2a (hộp kem)

Vì tổng số tiền mua kem của hai bạn là 624 nghìn đồng nên ta có phương trình:

32a + 24 + 32.2a + 24 = 624

Û 96a = 576 Û a = 6 (thỏa mãn).

Vậy Bình mua 6 hộp kem.

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 1)

12 câu hỏi 90 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 2)

12 câu hỏi 90 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 3)

16 câu hỏi 90 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 4)

16 câu hỏi 90 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 5)

6 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 7)

16 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 8)

5 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 9)

4 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 10)

5 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 11)

5 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 12)

5 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 13)

18 câu hỏi 45 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 14)

5 câu hỏi 90 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 15)

4 câu hỏi 90 phút

Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 16)

6 câu hỏi 90 phút

Các bài thi hot trong chương:

Đề kiểm tra 1 tiết Toán 9 Chương 3 Đại số có đáp án

( 4.4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 3 Đại số có đáp án

( 4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 4 Đại Số có đáp án

( 4.1 K lượt thi )

Đề kiểm tra 1 tiết Toán 9 Chương 4 Đại số có đáp án

( 2.9 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 3 Hình học có đáp án

( 4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 1 Đại Số (có đáp án)

( 8.5 K lượt thi )

Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án

( 7.4 K lượt thi )

Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023

( 6.4 K lượt thi )

Đề kiểm tra 15 phút Toán 9 Chương 1 Hình học có đáp án

( 6.1 K lượt thi )

Đề kiểm tra 1 tiết Toán 9 Chương 1 Đại Số có đáp án

( 5.4 K lượt thi )

Đánh giá trung bình

Thi Online Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án