Câu hỏi:
13/07/2024 6,828
(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Chứng minh tứ giác ABOC nội tiếp và OH.OA = R2.
b) Kẻ dây cung BD của đường tròn (O; R) song song với AO. Đoạn AD cắt (O; R) tại E (khác D). Gọi F là trung điểm của DE. Chứng minh tứ giác ABFO nội tiếp và tam giác BEF vuông.
c) Kẻ đường kính BK của đường tròn (O; R). Chứng minh tia AO là phân giác của góc DAK.
(3,0 điểm) Cho đường tròn tâm O, bán kính R và điểm A ở ngoài đường tròn (O; R) sao cho AO > 2R. Kẻ 2 tiếp tuyến AB, AC (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC.
a) Chứng minh tứ giác ABOC nội tiếp và OH.OA = R2.
b) Kẻ dây cung BD của đường tròn (O; R) song song với AO. Đoạn AD cắt (O; R) tại E (khác D). Gọi F là trung điểm của DE. Chứng minh tứ giác ABFO nội tiếp và tam giác BEF vuông.
c) Kẻ đường kính BK của đường tròn (O; R). Chứng minh tia AO là phân giác của góc DAK.
Câu hỏi trong đề:
Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
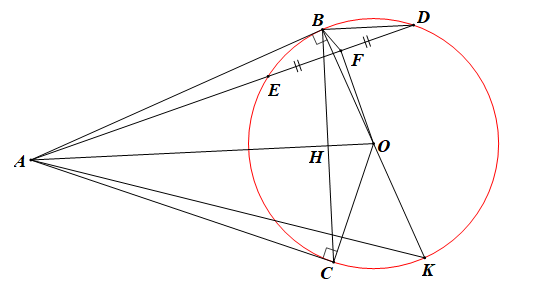
a) Ta có: AB, AC là 2 tiếp tuyến
Þ AB ^ OB; AC ^ OC
Xét tứ giác ABOC có
Þ Hai điểm B và C cùng nằm trên đường tròn đường kính AO
Þ Tứ giác ABOC nội tiếp đường tròn đường kính AO.
Vì AB, AC là hai tiếp tuyến của (O) cắt nhau tại A
Nên AB = AC và OB = OC (tính chất hai tiếp tuyến cắt nhau)
Suy ra A và O cùng nằm trên đường trung trực của BC
Do đó AO là đường trung trực của BC.
Þ AO ⊥ BC.
Xét ∆ABO vuông tại B ( ), BH ^ AO (BC ^ AO, H Î BC)
Theo hệ thức lượng trong tam giác vuông ta có:
OB2 = OH.OA
Þ OH.OA = R2.
b) F là trung điểm ED
Þ OF ^ ED (liên hệ giữa dây cung và đường kính)
Xét tứ giác ABFO có
Mà và là hai góc có đỉnh kề nhau của tứ giác ABFO
Þ Tứ giác ABFO nội tiếp
Þ (hai góc nội tiếp cùng chắn cung AB)
Mà (2 góc cùng chắn cung BD) và (Tam giác OBC cân tại O).
=>
Mà (do ∆BHO vuông tại H).
Þ
Þ Tam giác BEF vuông tại B.
c) Xét ∆ABO và ∆ACO có :
AO chung,
OB = OC = R,
Þ ∆ABO = ∆ACO (cạnh huyền – cạnh góc vuông)
Þ (hai góc tương ứng)
Mà BD // AO Þ BD ^ BC
Þ
Þ CD là đường kính của (O)
Xét ∆BDC và ∆CBK có:
CD = BK = 2R,
,
BC chung,
Þ ∆BDC = ∆CBK (cạnh huyền – cạnh góc vuông)
Þ BD = CK
Ta có:
Mà (hai góc nội tiếp cùng chắn cung DK)
Xét ∆ABD và ∆ACK có:
AB = AC (chứng minh câu a),
(chứng minh trên),
BD = CK
Þ ∆ABD = ∆ACK (c.g.c)
Þ (hai góc tương ứng)
Tam giác ABC có AB = AC (chứng minh trên)
Nên DABC cân tại A
(tính chất tam giác cân)
=>
Þ AO là phân giác góc DAK.
Vậy AO là phân giác góc DAK.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
(0,5 điểm) Từ một tấm tôn hình chữ nhật, kích thước 50cm x 189cm người ta cuộn tròn lại thành mặt xung quanh của một hình trụ cao 50 cm (như hình bên).
Hãy tính bán kính r của đường tròn đáy và thể tích của hình trụ (kết quả làm tròn đến hàng dơn vị). Biết: diện tích xung quanh của hình trụ bằng 2prh, thể tích hình trụ bằng pr2h (h là chiều cao của hình trụ).
(0,5 điểm) Từ một tấm tôn hình chữ nhật, kích thước 50cm x 189cm người ta cuộn tròn lại thành mặt xung quanh của một hình trụ cao 50 cm (như hình bên).
Hãy tính bán kính r của đường tròn đáy và thể tích của hình trụ (kết quả làm tròn đến hàng dơn vị). Biết: diện tích xung quanh của hình trụ bằng 2prh, thể tích hình trụ bằng pr2h (h là chiều cao của hình trụ).
Xem đáp án »
13/07/2024
6,220
Câu 2:
(1,5 điểm) Cho phương trình: x2 + 2mx + m2 + 2m – 2 = 0 (1) (x là ẩn).
a) Tìm giá trị của m để phương trình (1) có hai nghiệm.
b) Gọi x1, x2 là hai nghiệm của phương trình (1). Tìm giá trị của m để x1x2 + x1 + x2 = 0.
(1,5 điểm) Cho phương trình: x2 + 2mx + m2 + 2m – 2 = 0 (1) (x là ẩn).
a) Tìm giá trị của m để phương trình (1) có hai nghiệm.
b) Gọi x1, x2 là hai nghiệm của phương trình (1). Tìm giá trị của m để x1x2 + x1 + x2 = 0.
Xem đáp án »
13/07/2024
5,715
Câu 3:
(1,0 điểm) Một cửa hàng bán loại kem lạnh A như sau: nếu mua không quá 3 hộp thì giá 40 nghìn đồng mỗi hộp, nếu mua nhiều hơn 3 hộp thì bắt đầu từ hộp thứ tư trở đi giá mỗi hộp sẽ giảm đi 20% so với giá ban đầu.
a) Viết công thức tính y (số tiền mua kem) theo x (số hộp kem mua được trong trường hợp mua nhiều hơn 3 hộp).
b) An và Bình đều mua loại kem lạnh A với số hộp nhiều hơn 3. Biết rằng số hộp kem An mua gấp đôi số hộp Bình mua, đồng thời tổng số tiền mua kem của hai bạn là 624 nghìn đồng, hỏi bạn Bình mua bao nhiêu hộp kem? Giải thích.
(1,0 điểm) Một cửa hàng bán loại kem lạnh A như sau: nếu mua không quá 3 hộp thì giá 40 nghìn đồng mỗi hộp, nếu mua nhiều hơn 3 hộp thì bắt đầu từ hộp thứ tư trở đi giá mỗi hộp sẽ giảm đi 20% so với giá ban đầu.
a) Viết công thức tính y (số tiền mua kem) theo x (số hộp kem mua được trong trường hợp mua nhiều hơn 3 hộp).
b) An và Bình đều mua loại kem lạnh A với số hộp nhiều hơn 3. Biết rằng số hộp kem An mua gấp đôi số hộp Bình mua, đồng thời tổng số tiền mua kem của hai bạn là 624 nghìn đồng, hỏi bạn Bình mua bao nhiêu hộp kem? Giải thích.
Xem đáp án »
12/07/2024
3,748
Câu 4:
(1,0 điểm) Lớp 9A có 42 học sinh. Vừa qua lớp đã phát động phong trào tặng sách cho các bạn khó khăn ở vùng sâu. Tại buổi phát động, mỗi học sinh trong lớp đều tặng 3 quyển sách hoặc 5 quyển sách. Kết quả cả lớp đã tặng được 146 quyển sách. Hỏi lớp 9A có bao nhiêu bạn tặng 3 quyển sách và bao nhiêu bạn tặng 5 quyển sách?
(1,0 điểm) Lớp 9A có 42 học sinh. Vừa qua lớp đã phát động phong trào tặng sách cho các bạn khó khăn ở vùng sâu. Tại buổi phát động, mỗi học sinh trong lớp đều tặng 3 quyển sách hoặc 5 quyển sách. Kết quả cả lớp đã tặng được 146 quyển sách. Hỏi lớp 9A có bao nhiêu bạn tặng 3 quyển sách và bao nhiêu bạn tặng 5 quyển sách?
Xem đáp án »
13/07/2024
1,897
Câu 5:
(1,5 điểm)
a) Vẽ đồ thị (P) của hàm số y = và đồ thị (D) của hàm số y = −3x – 4 trên cùng hệ trục tọa độ.
b) Tính tọa độ các giao điểm của đồ thị (P) và đồ thị (D).
(1,5 điểm)
a) Vẽ đồ thị (P) của hàm số y = và đồ thị (D) của hàm số y = −3x – 4 trên cùng hệ trục tọa độ.
b) Tính tọa độ các giao điểm của đồ thị (P) và đồ thị (D).
Xem đáp án »
12/07/2024
815
Câu 6:
(1,5 điểm) Giải các phương trình
a) 2x2 – 5x + 2 = 0;
b) x4 + x2 – 6 = 0.
(1,5 điểm) Giải các phương trình
a) 2x2 – 5x + 2 = 0;
b) x4 + x2 – 6 = 0.
Xem đáp án »
12/07/2024
240
về câu hỏi!