Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) 2x2 – 5x + 2 = 0
Cách 1:
Ta có D = (–5)2 – 4.2.2 = 9 > 0
Khi đó phương trình đã cho có hai nghiệm phân biệt
và
Vậy phương trình đã cho có tập nghiệp
Cách 2:
2x2 – 5x + 2 = 0
Û x2 − x + 1 = 0
Û x2 − x – 2x + 1 = 0
Û x − 2 = 0
Û (x – 2) = 0
Û Û .
Vậy phương trình đã cho có tập nghiệp
b) x4 + x2 – 6 = 0 (1)
Đặt t = x2 (t ≥ 0), phương trình (1) trở thành:
t2 + t – 6 = 0 (2)
Ta có hai cách giải phương trình (2) như sau:
Cách 1:
Ta có D = 12 – 4.1.(–6) = 25 > 0
Khi đó phương trình đã cho có hai nghiệm phân biệt là:
(thỏa mãn) và (không thỏa mãn)
Cách 2:
t2 + t – 6 = 0 (2)
Û t2 – 2t + 3t – 6 = 0
Û t(t – 2) + 3(t – 2) = 0
Û (t – 2)(t + 3) = 0
Û
Û t = 2 (thỏa mãn) hay t = −3 (không thỏa mãn).
Với t = 2, ta có: x2 = 2
Û x = hoặc x = .
Vậy phương trình đã cho có tập nghiệm
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
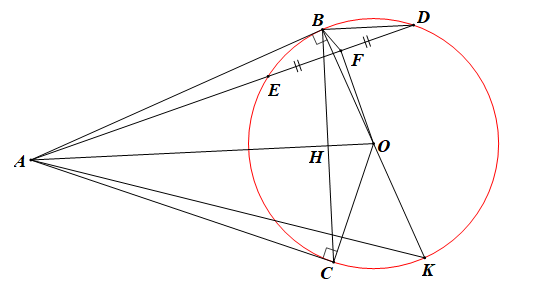
a) Ta có: AB, AC là 2 tiếp tuyến
Þ AB ^ OB; AC ^ OC
Xét tứ giác ABOC có
Þ Hai điểm B và C cùng nằm trên đường tròn đường kính AO
Þ Tứ giác ABOC nội tiếp đường tròn đường kính AO.
Vì AB, AC là hai tiếp tuyến của (O) cắt nhau tại A
Nên AB = AC và OB = OC (tính chất hai tiếp tuyến cắt nhau)
Suy ra A và O cùng nằm trên đường trung trực của BC
Do đó AO là đường trung trực của BC.
Þ AO ⊥ BC.
Xét ∆ABO vuông tại B ( ), BH ^ AO (BC ^ AO, H Î BC)
Theo hệ thức lượng trong tam giác vuông ta có:
OB2 = OH.OA
Þ OH.OA = R2.
b) F là trung điểm ED
Þ OF ^ ED (liên hệ giữa dây cung và đường kính)
Xét tứ giác ABFO có
Mà và là hai góc có đỉnh kề nhau của tứ giác ABFO
Þ Tứ giác ABFO nội tiếp
Þ (hai góc nội tiếp cùng chắn cung AB)
Mà (2 góc cùng chắn cung BD) và (Tam giác OBC cân tại O).
=>
Mà (do ∆BHO vuông tại H).
Þ
Þ Tam giác BEF vuông tại B.
c) Xét ∆ABO và ∆ACO có :
AO chung,
OB = OC = R,
Þ ∆ABO = ∆ACO (cạnh huyền – cạnh góc vuông)
Þ (hai góc tương ứng)
Mà BD // AO Þ BD ^ BC
Þ
Þ CD là đường kính của (O)
Xét ∆BDC và ∆CBK có:
CD = BK = 2R,
,
BC chung,
Þ ∆BDC = ∆CBK (cạnh huyền – cạnh góc vuông)
Þ BD = CK
Ta có:
Mà (hai góc nội tiếp cùng chắn cung DK)
Xét ∆ABD và ∆ACK có:
AB = AC (chứng minh câu a),
(chứng minh trên),
BD = CK
Þ ∆ABD = ∆ACK (c.g.c)
Þ (hai góc tương ứng)
Tam giác ABC có AB = AC (chứng minh trên)
Nên DABC cân tại A
(tính chất tam giác cân)
=>
Þ AO là phân giác góc DAK.
Vậy AO là phân giác góc DAK.
Lời giải
x2 + 2mx + m2 + 2m – 2 = 0 có a = 1, b = 2m, c = m2 + 2m – 2
Ta có:
∆ = b2 – 4ac
= (2m)2 – 4.1.(m2 + 2m – 2)
= -8m + 8
a) Để phương trình (1) có hai nghiệm Û ∆ ≥ 0
Û −8m + 8 ≥ 0 Û m ≤ 1.
Vậy với m ≤ 1 thì phương trình (1) có hai nghiệm.
b) Với m ≤ 1, phương trình (1) có hai nghiệm x1, x2
Theo hệ thức Vi – ét ta có:
Ta có: x1x2 + x1 + x2 = 0
Û m2 + 2m – 2 – 2m = 0
Û m2 = 2
Û m = (không thỏa mãn) hoặc m = (thỏa mãn)
Vậy m = thỏa mãn yêu cầu bài toán.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo