Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 12)

🔥 Học sinh cũng đã học

84 người thi tuần này

Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Thực Nghiệm Khoa học Giáo dục (Hà Nội) có đáp án

314 lượt thi 7 câu hỏi

36 người thi tuần này

Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Hoàng Hoa Thám (Hà Nội) có đáp án

266 lượt thi 6 câu hỏi

33 người thi tuần này

Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Hoàng Hoa Thám (Hà Nội) có đáp án

263 lượt thi 7 câu hỏi

32 người thi tuần này

Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Giảng Võ (Hà Nội) có đáp án

262 lượt thi 6 câu hỏi

45 người thi tuần này

Đề thi giữa kì 1 Toán 9 năm 2025-2026 THCS Lê Quý Đôn (Hà Nội) có đáp án

275 lượt thi 7 câu hỏi

477 người thi tuần này

Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 19

4.5 K lượt thi 53 câu hỏi

149 người thi tuần này

Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 18

4.2 K lượt thi 100 câu hỏi

98 người thi tuần này

Trắc nghiệm Tổng hợp Toán năm 2024 có đáp án - Phần 17

4.1 K lượt thi 100 câu hỏi

Danh sách câu hỏi:

Câu 1/5

1) Giải hệ phương trình $\{\begin{matrix} 2 x - y = 1 \\ x + 2 y = 8 \end{matrix}$ .

2) Giải phương trình x²+ x – 6 = 0.

3) Giải phương trình x⁴ – x² – 12 = 0.

Xem đáp án

Lời giải

1) $\{\begin{matrix} 2 x - y = 1 \\ x + 2 y = 8 \end{matrix}$

Û $\{\begin{matrix} 2 x - y = 1 \\ 2 x + 4 y = 16 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 5 y = 15 \\ 2 x - y = 1 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x = 2 \\ y = 3 \end{matrix}$

Vậy hệ phương trình đã cho có nghiệm là (2; 3).

2) x²+ x – 6 = 0

Û x² – 2x + 3x – 6 = 0

Û x(x – 2) + 3(x – 2) = 0

Û (x – 2)(x + 3) = 0

Û $[\begin{matrix} x - 2 = 0 \\ x + 3 = 0 \end{matrix}$

Û $[\begin{matrix} x = 2 \\ x = - 3 \end{matrix}$ .

Vậy tập phương trình đã cho là S = {2; −3}.

3) x⁴ – x² – 12 = 0 (1)

Đặt t = x² (t ≥ 0), phương trình (1) trở thành:

t² – t – 12 = 0

Û t² + 3t – 4t – 12 = 0

Û t(t + 3) – 4(t + 3) = 0

Û (t – 4)(t + 3) = 0

Û t – 4 = 0 hay t + 3 = 0

Û t = 4 (nhận) hay t = −3 (loại)

Ta có: x² = 4 Û x = 2 hay x = −2.

Vậy tập phương trình đã cho là S = {2; −2}.

Câu 2/5

Cho hàm số y = 2x² có đồ thị là (P).

1) Xét tính đồng biến, nghịch biến của hàm số đã cho và vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.

2) Tìm tọa độ của điểm M thuộc đồ thị (P) biết M có hoành độ bằng 3.

Xem đáp án

Lời giải

1) Hàm số y = 2x² có hệ số a = 2 > 0. Vậy hàm số y = 2x² đồng biến khi x > 0.

Vẽ (P)

Bảng giá trị

x	−1		0		1
y = 2x²	2		0		2

Trên mặt phẳng tọa độ lấy các điểm: A(−1; 2); B $(- \frac{1}{2}; \frac{1}{2})$ ; O(0; 0), C $(\frac{1}{2}; \frac{1}{2})$ ,D(1; 2).

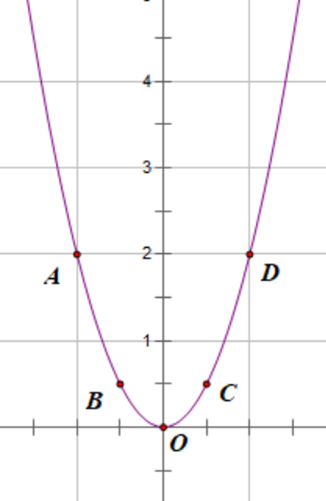
Cho hàm số y = 2x2 có đồ thị là (P). 1) Xét tính đồng biến, nghịch biến của hàm số đã cho và vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy. 2) Tìm tọa độ của điểm M thuộc đồ thị (P) biết M có hoành độ bằng 3. (ảnh 1)

2) Ta có M(3; y_M) Î (P)

Thay M(3; y_M) vào (P), ta được: y_M = 2.3² = 18

Vậy tọa độ điểm M là (3; 18).

Câu 3/5

1) Cho phương trình x² – 6x + m = 0 (với m là tham số).

Tìm m để phương trình đã cho có nghiệm kép và tìm nghiệm kép đó.

2) Cho x₁ và x₂ là hai nghiệm của phương trình x² – 3x – 2 = 0.

Tính giá trị của biểu thức P = x₁² + x₂².

Xem đáp án

Lời giải

1) x² – 6x + m = 0 (a = 1, b = −6, c = m)

Ta có: ∆ = b² – 4ac = (−6)² – 4.1.m = 36 – 4m

Để phương trình có nghiệm kép thì ∆ = 0 Û 36 – 4m = 0

Û 4m = 36 Û m = 9.

Thay m = 9 vào phương trình trên ta được:

x² – 6x + 9 = 0

Û (x – 3)² = 0 Û x = 3.

Vậy để phương trình đã cho có nghiệm kép thì m = 9 và nghiệm kép là x = 3.

2) x² – 3x – 2 = 0 (a = 1, b = −3, c = −2)

Theo hệ thức Vi – ét, ta có: $\{\begin{matrix} x_{1} + x_{2} = \frac{- b}{a} = 3 \\ x_{1} x_{2} = \frac{c}{a} = - 2 \end{matrix}$

Ta có: P = x₁² + x₂² = (x₁ + x₂)² − 2x₁x₂ = 3² – 2.(−2) = 13.
Vậy P = x₁² + x₂² = 13.

Câu 4/5

1) Tính diện tích toàn phần của hình trụ có chiều cao bằng 3 dm và bán kính đáy bằng 2 dm (học sinh không cần vẽ hình khi giải câu này).

2) Bác Thành có một khu vườn hình chữ nhật biết chiều dài hơn chiều rộng 10m và diện tích bằng 1200 m²; bác Thành xây bức tường bao quanh khu vườn, xây theo chu vi của khu vườn, với giá thành được tính mỗi mét của bức tường đo theo chu vi của khu vườn (bên ngoài) có giá là 700 nghìn đồng, không kể phần cổng của khu vườn dài 3 mét. Tính số tiền bác Thành dùng để xây bức tường nói trên.

Xem đáp án

Lời giải

1) Diện tích toàn phần của hình trụ là:

S_tp = 2pR.h + 2p.R² = 2.2.3p + 2p.2² = 20p (dm²).

Vậy diện tích toàn phần của hình trụ là 20p dm².

2) Gọi x (m) là chiều dài khu vườn (x > 10)

Chiều rộng khu vườn là x – 10 (m).

Theo đề bài ta có phương trình: x(x – 10) = 1200

Û x² – 10x – 1200 = 0

Û x² – 40x + 30x – 1200 = 0

Û x(x – 40) + 30(x – 40) = 0

Û (x – 40)(x + 30) = 0

Û x – 40 = 0 hay x + 30 = 0

Û x = 40 (nhận) hay x = −30 (loại).

Chiều dài khu vườn là 40m, chiều rộng khu vườn là 40 – 10 = 30 (m).

Chu vi khu vườn là:

(40 + 30).2 = 140 (m).

Số tiền bác Thành dùng để xây bức tường là:

700 000.(140 – 3) = 95 900 000 (đồng).

Vậy số tiền bác Thành dùng để xây bức tường là 95 900 000 đồng.

Câu 5/5

Cho tam giác nhọn ABC có hai đường cao BE và CF cắt nhau tại điểm H.

1) Chứng minh tứ giác AEHF nội tiếp đường tròn.

2) Chứng minh $\hat{F E C} + \hat{A B C} = 180 °$ .

3) Gọi D là giao điểm của hai đường thẳng AH và BC. Chứng minh H là tâm của đường tròn nội tiếp tam giác DEF.

Xem đáp án

Lời giải

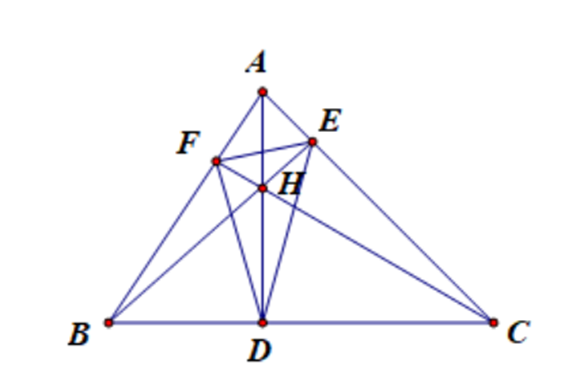
Cho tam giác nhọn ABC có hai đường cao BE và CF cắt nhau tại điểm H. 1) Chứng minh tứ giác AEHF nội tiếp đường tròn. (ảnh 1)

1) Xét tứ giác AEHF, có $\hat{A E H} + \hat{A F H} = 180 °$ mà hai góc ở vị trí đối nhau.

Vậy tứ giác AEHF nội tiếp

2) Xét tứ giác BFEC, có: $\hat{B F C} = \hat{B E C} = 90 °$ mà hai góc cùng nhìn cạnh BC.

Suy ra tứ giác BFEC nội tiếp.

Do đó $\hat{F E C} + \hat{F B C} = 180 °$ .

Vậy $\hat{F E C} + \hat{A B C} = 180 °$ .

3) Tam giác ABC có BE ^ AC; CF ^ AB, BE và CF cắt nhau tại H.

Suy ra H là trực tâm tam giác ABC nên AH ^ BC tại D.

Khi đó $\{\begin{matrix} \hat{H E C} + \hat{H D C} = 180 ° \\ \hat{H F B} + \hat{H D B} = 180 ° \end{matrix}$

Do đó tứ giác BFHD và CEHD nội tiếp.

+ Tứ giác AEHF nội tiếp Þ $\hat{F A H} = \hat{F E H}$ Þ $\hat{F E H} = \hat{B A D}$

Tứ giác CDHE nội tiếp Þ $\hat{H C D} = \hat{H E D}$ Þ $\hat{H E D} = \hat{B C F}$

Mà $\hat{B C F} = \hat{B A D}$ (cùng phụ $\hat{B}$ )

Þ $\hat{F E H} = \hat{D E H}$ Þ EH là phân giác góc DEF.

+ Tứ giác AEHF nội tiếp Þ $\hat{E F H} = \hat{H A E}$ Þ $\hat{E F H} = \hat{D A C}$

Tứ giác BFHD nội tiếp Þ $\hat{H F D} = \hat{H B D}$ Þ $\hat{H F D} = \hat{E B C}$

Mà $\hat{E B C} = \hat{D A C}$ (cùng phụ $\hat{C}$ )

Þ $\hat{H F E} = \hat{H F D}$

Þ FH là phân giác góc DFE

Mà FH và EH cắt nhau tại H

Þ H là tâm đường tròn nội tiếp tam giác DEF.

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

1) Giải hệ phương trình $\{\begin{matrix} 2 x - y = 1 \\ x + 2 y = 8 \end{matrix}$ .

2) Giải phương trình x²+ x – 6 = 0.

3) Giải phương trình x⁴ – x² – 12 = 0.

Cho hàm số y = 2x² có đồ thị là (P).

1) Xét tính đồng biến, nghịch biến của hàm số đã cho và vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.

2) Tìm tọa độ của điểm M thuộc đồ thị (P) biết M có hoành độ bằng 3.

1) Cho phương trình x² – 6x + m = 0 (với m là tham số).

Tìm m để phương trình đã cho có nghiệm kép và tìm nghiệm kép đó.

2) Cho x₁ và x₂ là hai nghiệm của phương trình x² – 3x – 2 = 0.

Tính giá trị của biểu thức P = x₁² + x₂².