Cho hàm số y = 2x2 có đồ thị là (P).
1) Xét tính đồng biến, nghịch biến của hàm số đã cho và vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.
2) Tìm tọa độ của điểm M thuộc đồ thị (P) biết M có hoành độ bằng 3.
Cho hàm số y = 2x2 có đồ thị là (P).
1) Xét tính đồng biến, nghịch biến của hàm số đã cho và vẽ đồ thị (P) trên mặt phẳng tọa độ Oxy.
2) Tìm tọa độ của điểm M thuộc đồ thị (P) biết M có hoành độ bằng 3.
Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
1) Hàm số y = 2x2 có hệ số a = 2 > 0. Vậy hàm số y = 2x2 đồng biến khi x > 0.
Vẽ (P)
Bảng giá trị
|
x |
−1 |
|
0 |
|
1 |
|
y = 2x2 |
2 |
|
0 |
|
2 |
Trên mặt phẳng tọa độ lấy các điểm: A(−1; 2); B ; O(0; 0), C ,D(1; 2).
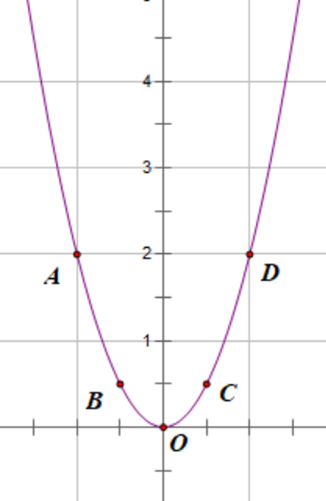
2) Ta có M(3; yM) Î (P)
Thay M(3; yM) vào (P), ta được: yM = 2.32 = 18
Vậy tọa độ điểm M là (3; 18).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
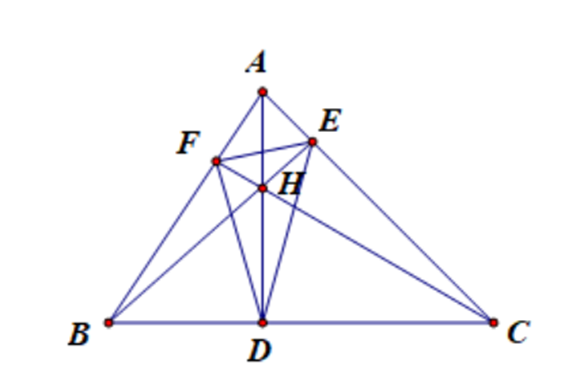
1) Xét tứ giác AEHF, có mà hai góc ở vị trí đối nhau.
Vậy tứ giác AEHF nội tiếp
2) Xét tứ giác BFEC, có: mà hai góc cùng nhìn cạnh BC.
Suy ra tứ giác BFEC nội tiếp.
Do đó .
Vậy .
3) Tam giác ABC có BE ^ AC; CF ^ AB, BE và CF cắt nhau tại H.
Suy ra H là trực tâm tam giác ABC nên AH ^ BC tại D.
Khi đó
Do đó tứ giác BFHD và CEHD nội tiếp.
+ Tứ giác AEHF nội tiếp Þ Þ
Tứ giác CDHE nội tiếp Þ Þ
Mà (cùng phụ )
Þ Þ EH là phân giác góc DEF.
+ Tứ giác AEHF nội tiếp Þ Þ
Tứ giác BFHD nội tiếp Þ Þ
Mà (cùng phụ )
Þ
Þ FH là phân giác góc DFE
Mà FH và EH cắt nhau tại H
Þ H là tâm đường tròn nội tiếp tam giác DEF.
Lời giải
1) x2 – 6x + m = 0 (a = 1, b = −6, c = m)
Ta có: ∆ = b2 – 4ac = (−6)2 – 4.1.m = 36 – 4m
Để phương trình có nghiệm kép thì ∆ = 0 Û 36 – 4m = 0
Û 4m = 36 Û m = 9.
Thay m = 9 vào phương trình trên ta được:
x2 – 6x + 9 = 0
Û (x – 3)2 = 0 Û x = 3.
Vậy để phương trình đã cho có nghiệm kép thì m = 9 và nghiệm kép là x = 3.
2) x2 – 3x – 2 = 0 (a = 1, b = −3, c = −2)
Theo hệ thức Vi – ét, ta có:
Ta có: P = x12 + x22 = (x1 + x2)2 − 2x1x2 = 32 – 2.(−2) = 13.
Vậy P = x12 + x22 = 13.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.